Número perfecto para niños

Un número perfecto es un número entero positivo que tiene una característica muy especial: es igual a la suma de todos sus divisores, ¡pero sin contarse a sí mismo! Imagina que tienes un número y encuentras todos los números que lo dividen exactamente. Si sumas esos divisores (excepto el número original), y el resultado es el número original, ¡entonces es un número perfecto!

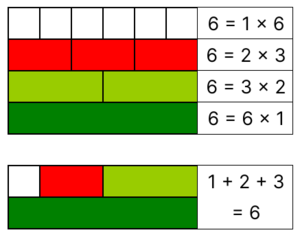
Por ejemplo, el número 6 es un número perfecto. Sus divisores son 1, 2, 3 y 6. Si sumamos sus divisores propios (los que no son el 6), obtenemos: 1 + 2 + 3 = 6. ¡Es perfecto!

Otros ejemplos de números perfectos son:

• 28: Sus divisores propios son 1, 2, 4, 7, 14. La suma es 1 + 2 + 4 + 7 + 14 = 28.
• 496: Sus divisores propios son 1, 2, 4, 8, 16, 31, 62, 124, 248. La suma es 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496.
• 8128: Sus divisores propios son 1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064. La suma es 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064 = 8128.

Ilustración con regletas de Cuisenaire de que el 6 es un número perfecto.

Historia de los números perfectos

Los números perfectos han fascinado a los matemáticos desde la antigüedad.

Descubrimientos de Euclides

El famoso matemático griego Euclides, hace más de 2000 años, descubrió una fórmula para encontrar algunos números perfectos pares. Su fórmula es .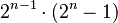

Euclides notó que si el número Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^{n}-1 es un número primo (un número que solo se puede dividir por 1 y por sí mismo), entonces al usar su fórmula, el resultado siempre será un número perfecto par.

Veamos cómo funciona con los primeros números perfectos:

• Si n = 2: 2¹ × (2² – 1) = 2 × (4 – 1) = 2 × 3 = 6
• Si n = 3: 2² × (2³ – 1) = 4 × (8 – 1) = 4 × 7 = 28
• Si n = 5: 2⁴ × (2⁵ – 1) = 16 × (32 – 1) = 16 × 31 = 496
• Si n = 7: 2⁶ × (2⁷ – 1) = 64 × (128 – 1) = 64 × 127 = 8128

En todos estos casos, el número Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^{n}-1 (que son 3, 7, 31 y 127) es un número primo.

Suposiciones antiguas y nuevos hallazgos

Los matemáticos de la antigüedad hicieron algunas suposiciones sobre los números perfectos basándose en los pocos que conocían. Sin embargo, muchas de estas ideas resultaron ser incorrectas.

Por ejemplo, pensaron que el quinto número perfecto se obtendría con n = 11 (porque 2, 3, 5 y 7 son los primeros cuatro números primos). Pero Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^{11}-1 es 2047, y este número no es primo (se puede dividir por 23 y por 89). Así que n = 11 no genera un número perfecto.

También creyeron que los números perfectos tendrían un número de dígitos que aumentaría de uno en uno (1, 2, 3, 4 dígitos) y que terminarían alternativamente en 6 y en 8.

El quinto número perfecto, que es 33 550 336, tiene 8 dígitos, lo que desmintió la primera suposición. Además, el sexto número perfecto (8 589 869 056) también termina en 6, rompiendo la idea de la alternancia entre 6 y 8.

En el año 1603, el matemático Pietro Cataldi encontró el sexto y el séptimo número perfecto.

Números primos de Mersenne

Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^{n}-1 es un número primo, entonces n también debe ser un número primo. A estos números primos de la forma Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^{n}-1 se les llama números primos de Mersenne, en honor a Marin Mersenne, un monje del siglo XVII que los estudió.

En el siglo XVIII, el matemático Leonhard Euler demostró algo muy importante: que todos los números perfectos pares se pueden encontrar usando la fórmula que Euclides había descubierto.

¿Existen números perfectos impares?

Hasta ahora, no se ha encontrado ningún número perfecto impar. Los matemáticos han investigado mucho sobre esto y han descubierto que, si existiera un número perfecto impar, tendría que ser muy, muy grande (más de 10³⁰⁰) y tener muchas características especiales. Es una de las grandes preguntas sin respuesta en las matemáticas.

El número perfecto más grande conocido

El 7 de diciembre de 2018, se descubrió el número primo más grande conocido hasta esa fecha, que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^{82 589 933}-1 . Gracias a este descubrimiento, se pudo encontrar el número perfecto más grande conocido, el número 51 de la lista. Este número es gigantesco, ¡tiene casi 50 millones de dígitos!

Este gran número primo fue descubierto por Patrick Laroche como parte de un proyecto llamado Great Internet Mersenne Prime Search (GIMPS), donde muchas personas usan sus computadoras para buscar números primos.

Características de los números perfectos pares

Los números perfectos pares tienen algunas propiedades interesantes.

Son números triangulares

Un número triangular es un número que se puede representar como un triángulo de puntos. Por ejemplo, 1, 3, 6, 10 son números triangulares. Resulta que todos los números perfectos pares son también números triangulares.

Son números hexagonales

Un número hexagonal es un número que se puede representar como un hexágono de puntos. Los números perfectos pares también son números hexagonales.

Preguntas sin respuesta sobre los números perfectos

En matemáticas, una "cuestión abierta" es un problema que aún no tiene una solución o una demostración. Aquí hay algunas preguntas sin respuesta sobre los números perfectos:

• ¿Existen infinitos números perfectos? Hasta octubre de 2024, se conocen 52 números perfectos.
• ¿Existe algún número perfecto impar? Nadie ha encontrado uno, ni se ha demostrado que no puedan existir.

Otros tipos de números relacionados

Además de los números perfectos, existen otros tipos de números que se clasifican según la suma de sus divisores:

• Números defectivos: La suma de sus divisores propios es menor que el número. Por ejemplo, el 4 (divisores propios: 1, 2; suma: 1+2=3, que es menor que 4).
• Números abundantes: La suma de sus divisores propios es mayor que el número. Por ejemplo, el 12 (divisores propios: 1, 2, 3, 4, 6; suma: 1+2+3+4+6=16, que es mayor que 12).
• Números amigos: Son dos números diferentes donde la suma de los divisores propios de uno es igual al otro número, y viceversa. Por ejemplo, 220 y 284.
• Números sociables: Son como los números amigos, pero forman una cadena o ciclo de más de dos números.
• Números semiperfectos: Son números donde la suma de algunos de sus divisores propios es igual al número.

Véase también

En inglés: Perfect number Facts for Kids

• Números amigos
• Números sociables
• Números primos de Mersenne y números perfectos