Método neusis para niños
La Neusis es un método especial que usaban los matemáticos de la antigua Grecia para resolver problemas de geometría. Imagina que tienes una regla con dos marcas. Con la Neusis, debes mover esa regla de una forma muy específica: una marca debe tocar una línea o curva, la otra marca debe tocar otra línea o curva, y la regla (o su extensión) debe pasar por un punto fijo.
Este método era como un "as bajo la manga" para los griegos. No lo usaban siempre, solo cuando los problemas eran muy difíciles y no se podían resolver con las herramientas más comunes: la regla y compás. Con la regla y compás, solo puedes dibujar líneas rectas y círculos, sin medir distancias preestablecidas en la regla.
Contenido
¿Cómo funciona la construcción Neusis?
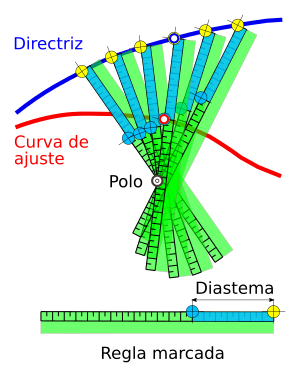
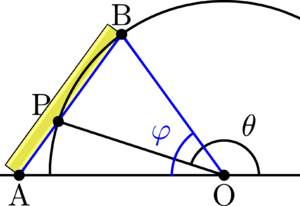
La palabra "Neusis" viene del griego y significa "inclinación" o "dirección". Para hacer una construcción Neusis, necesitas una regla especial, a la que podríamos llamar "regla Neusis".
Elementos clave de una construcción Neusis
Una construcción Neusis siempre tiene estos elementos:
- Un segmento de línea con una longitud fija: A esta longitud la llamaban diastema. Piensa en ella como la distancia que ya tienes marcada en tu regla.
- Dos curvas o líneas: Una es la "curva directriz" y la otra es la "curva de ajuste". Son los lugares donde deben tocar los extremos de tu segmento.
- Un punto fijo: A este punto lo llamaban "polo". Es el punto por donde debe pasar tu segmento o su prolongación.
Pasos para usar la regla Neusis
Imagina que tienes una regla que puede girar alrededor del "polo" (como si pusieras una chincheta en el polo y la regla girara sobre ella).
- En la regla, tienes una marca (como un círculo amarillo) que es el inicio de tu medida.
- Otra marca (como un círculo azul) indica la longitud de tu diastema.
- Mueves la regla: la marca amarilla se desliza por la "curva directriz".
- Al mismo tiempo, la marca azul debe coincidir con la "curva de ajuste".
- Cuando logras que ambas marcas estén en su lugar y la regla pase por el polo, ¡has encontrado la posición correcta del segmento!
¿Para qué se usaba la Neusis?
La Neusis era muy importante porque permitía resolver problemas de geometría que eran imposibles de solucionar solo con regla y compás.
Problemas resueltos con Neusis
Algunos ejemplos famosos de problemas que se podían resolver con Neusis son:
- Dividir un ángulo en tres partes iguales: Esto se llama "trisección del ángulo". Con regla y compás, solo se pueden dividir algunos ángulos, pero con Neusis, ¡se puede dividir cualquier ángulo!
- Construir un heptágono regular: Un heptágono es una figura de siete lados iguales. Con Neusis, se podía dibujar.
Matemáticos muy famosos como Arquímedes (que vivió hace más de 2000 años) usaban la Neusis con libertad. Incluso siglos después, Isaac Newton también la empleó. Sin embargo, con el tiempo, esta técnica se fue usando menos.
Polígonos construibles con Neusis
Se ha descubierto que muchos polígonos regulares (figuras con todos sus lados y ángulos iguales) se pueden construir usando la Neusis. Por ejemplo, polígonos de 7, 9, 11, 13, 14, 17, 19, 21, 22, 26, 27, 28, 33, 34, 35, 37, 38, 39, 42, 44, 45, 51, 52, 54, 55, 56, 57, 63, 65, 66, 68, 70, 73, 74, 76, 77, 78, 81, 85, 88, 91, 95, 97, 99, 102, 104, 105, 108, 109, 110, 111, 112, 114, 117, 119, 126, 128 lados, entre otros, pueden ser construidos con este método.
¿Por qué dejó de usarse la Neusis?
Con el tiempo, la Neusis fue perdiendo popularidad entre los matemáticos.
La preferencia por regla y compás
Algunos historiadores creen que matemáticos como Enópides de Quíos (hace unos 2400 años) fueron los primeros en preferir las construcciones solo con regla y compás. Más tarde, Hipócrates de Quíos y Euclides, en su famoso libro "Los Elementos", también evitaron usar la Neusis.
La jerarquía de las construcciones
Con la influencia de pensadores como Platón, se desarrolló una especie de "clasificación" para los métodos de construcción geométrica, de los más "puros" a los más "prácticos":
- Primer nivel: Construcciones solo con líneas rectas y círculos (regla y compás). Eran consideradas las más "nobles".
- Segundo nivel: Construcciones que usaban también las "secciones cónicas" (como elipses, parábolas e hipérbolas).
- Tercer nivel: Construcciones que necesitaban otras técnicas, como la Neusis.
Así, la Neusis se convirtió en un último recurso. Solo se usaba si los métodos de los niveles superiores no podían resolver el problema. El matemático griego Pappus de Alejandría (hace unos 1700 años) incluso dijo que usar Neusis cuando se podía haber usado un método más "respetable" era un "error".
Galería de imágenes
-
Trisección Neusis de un ángulo >135° para encontrar φ=θ/3, utilizando solo la longitud de la regla. El radio del arco es igual a la longitud de la regla. Para ángulos θ<135° se aplica la misma construcción, pero con P extendido más allá de AB
Véase también
En inglés: Neusis construction Facts for Kids
