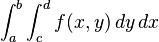Integral múltiple para niños

Una integral múltiple es una herramienta matemática que nos ayuda a calcular el "total" de algo que cambia en un espacio con varias dimensiones. Imagina que quieres saber el volumen de una montaña o la cantidad total de agua en un lago con una forma irregular. Las integrales múltiples nos permiten hacer eso.

Cuando trabajamos con funciones que dependen de dos variables (como 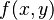), usamos integrales dobles. Estas nos ayudan a encontrar el volumen de una forma tridimensional o el área de una superficie. Si la función depende de tres variables (como 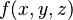), usamos integrales triples. Estas son útiles para calcular volúmenes en espacios más complejos.

La integral doble nos ayuda a calcular el volumen debajo de una superficie. La parte de abajo es el área sobre la que calculamos, y la superficie es la forma de la función.

¿Qué son las integrales múltiples?

Así como una integral normal (de una sola variable) puede calcular el área debajo de una línea en un gráfico, una integral doble puede calcular el volumen debajo de una superficie. Piensa en una superficie como el techo de una habitación. La integral doble nos diría cuánto espacio hay entre ese techo y el suelo.

Para funciones con más variables, las integrales múltiples nos permiten calcular "cantidades totales" en espacios más grandes. Por ejemplo, si una función describe la densidad de un material en diferentes puntos de un objeto, una integral triple nos daría la masa total de ese objeto.

La forma de escribir una integral múltiple es con varios símbolos de integral, uno dentro de otro. Por ejemplo, para una función de tres variables:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \iiint_D f(x,y,z)\;dx\,dy\,dz.

Aquí, 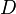representa la región del espacio donde estamos calculando. Es importante saber que las integrales múltiples siempre calculan un valor específico (como un volumen o un área), no una función general.

¿Cómo se calculan las integrales múltiples?

Calcular una integral múltiple es como sumar muchas partes muy pequeñas. Imagina que quieres saber el volumen de una piscina con una forma extraña. Podrías dividir la piscina en muchos cubitos muy pequeños. Si sabes la altura del agua en cada cubito, multiplicas esa altura por el área de la base del cubito para obtener el volumen de ese cubito. Luego, sumas el volumen de todos los cubitos.

Las integrales múltiples hacen esto de forma muy precisa. Dividen la región en la que estamos trabajando (como el fondo de la piscina) en partes infinitamente pequeñas. Luego, multiplican el valor de la función en cada parte por el tamaño de esa parte y suman todos esos resultados.

Integrales iteradas: el paso a paso

Para resolver una integral múltiple, la convertimos en lo que llamamos integrales iteradas. Esto significa que resolvemos una integral a la vez, de adentro hacia afuera.

Por ejemplo, para una integral doble:

Primero, resolvemos la integral de adentro (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \int_c^d f(x,y)\,dy ) tratando a como si fuera un número constante. El resultado de esta primera integral será una nueva función que solo depende de . Después, resolvemos la integral de afuera con esa nueva función.

Si la función es "bien portada" (matemáticamente hablando) y la región es sencilla, el orden en que integramos (primero Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): dy y luego 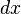, o al revés) no cambia el resultado final. Esto es muy útil porque a veces un orden es mucho más fácil de calcular que el otro.

Propiedades importantes

Las integrales múltiples tienen algunas propiedades que las hacen más fáciles de usar:

Suma y resta

Si tienes la integral de una suma o resta de funciones, puedes separarlas en la suma o resta de sus integrales individuales.

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \iint_D [f(x,y) \pm g(x,y)]\,dA = \iint_D f(x,y)\,dA \pm \iint_D g(x,y)\,dA

Multiplicación por un número

Si multiplicas una función por un número constante, puedes sacar ese número fuera de la integral.

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \iint_D c \cdot f(x,y)\,dA = c \cdot \iint_D f(x,y)\,dA

Regiones que se unen

Si la región sobre la que integras se puede dividir en dos partes que no se superponen, puedes calcular la integral en cada parte y luego sumar los resultados.

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \iint_{D_1 \cup D_2} f(x,y)\,dA = \iint_{D_1} f(x,y)\,dA + \iint_{D_2} f(x,y)\,dA

Métodos para calcular integrales múltiples

Integrar funciones constantes

Si la función que estás integrando es un número constante (por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x,y) = 5 ), la integral es muy sencilla. Solo tienes que multiplicar ese número por el "tamaño" de la región sobre la que estás integrando.

• Si es una integral doble y la región está en un plano, el "tamaño" es el área de esa región.
• Si es una integral triple y la región está en el espacio, el "tamaño" es el volumen de esa región.

Por ejemplo, si quieres calcular la integral doble de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x,y) = 2 sobre un rectángulo de 3 unidades de largo por 4 unidades de ancho, el resultado sería Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 \times (3 \times 4) = 2 \times 12 = 24 .

Usar la simetría

A veces, la forma de la región o la función que estamos integrando tienen simetría. Si una función es "impar" (com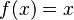o o 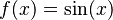) y la región es simétrica alrededor de un eje, la integral de esa parte de la función puede ser cero. Esto simplifica mucho los cálculos.

Por ejemplo, si integras Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x,y) = x sobre un círculo centrado en el origen, el resultado es cero porque por cada valor positivo de hay un valor negativo de que lo cancela.

Cambio de variables

A veces, la región sobre la que queremos integrar es complicada (por ejemplo, un círculo o una esfera). En estos casos, podemos "cambiar las coordenadas" para que la región se vuelva más sencilla, como un rectángulo. Esto se llama cambio de variables.

Cuando cambiamos las coordenadas, necesitamos un factor de ajuste llamado jacobiano. Este factor asegura que el "tamaño" de las pequeñas partes de la región se mantenga correcto después de la transformación.

Coordenadas polares

La transformación de coordenadas rectangulares a polares. Observa cómo el área cambia, lo que hace necesario el jacobiano.

Las coordenadas polares son muy útiles cuando la región de integración tiene forma de círculo o parte de un círculo. En lugar de usar e , usamos (la distancia al centro) y 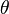(el ángulo).

Las relaciones son:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = r \cos(\theta)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = r \sin(\theta)

El factor de ajuste (jacobiano) para este cambio es . Así, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): dx\,dy se convierte en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): r\,dr\,d\theta .

Coordenadas cilíndricas

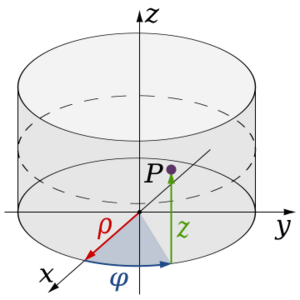
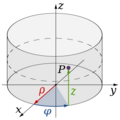
Gráfico de las Coordenadas Cilíndricas.

Las coordenadas cilíndricas son útiles para regiones que tienen forma de cilindro o partes de cilindro. Son como las coordenadas polares, pero le añadimos una altura .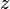

Las relaciones son:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = r \cos(\theta)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = r \sin(\theta)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z = z

El factor de ajuste (jacobiano) sigue siendo . Así, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): dx\,dy\,dz se convierte en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): r\,dr\,d\theta\,dz .

Coordenadas esféricas

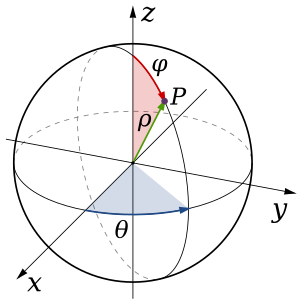
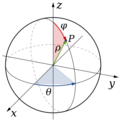
Gráfico de las coordenadas esféricas.

Las coordenadas esféricas son perfectas para regiones con forma de esfera o partes de esfera. Usamos 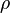(la distancia al origen), 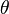(el ángulo alrededor del eje 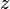, como en polares) y 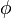(el ángulo desde el eje 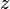positivo).

Las relaciones son:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = \rho \cos(\theta) \sin(\phi)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = \rho \sin(\theta) \sin(\phi)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z = \rho \cos(\phi)

El factor de ajuste (jacobiano) para este cambio es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \rho^2 \sin(\phi) . Así, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): dx\,dy\,dz se convierte en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \rho^2 \sin(\phi)\,d\rho\,d\theta\,d\phi .

Ejemplos de cálculo de volúmenes

Volumen de un cilindro

Podemos calcular el volumen de un cilindro con altura 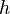y radio 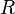usando una integral triple en coordenadas cilíndricas. La región del cilindro se describe como:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0 \leq r \leq R (radio)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0 \leq \theta \leq 2\pi (círculo completo)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0 \leq z \leq h (altura)

La integral para el volumen es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} V &= \iiint_D dV \\ &= \int_0^{2\pi}\int_0^R\int_0^h r\,dz\,dr\,d\theta \\ &= \int_0^{2\pi}d\theta \int_0^R r\,dr \int_0^h dz \\ &= (2\pi) \left(\frac{R^2}{2}\right) (h) \\ &= \pi R^2 h \end{align}

¡Este es el mismo resultado que la fórmula que ya conoces para el volumen de un cilindro!

Volumen de una esfera

También podemos calcular el volumen de una esfera de radio usando una integral triple en coordenadas esféricas. La región de la esfera se describe como:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0 \leq \rho \leq r (radio)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0 \leq \theta \leq 2\pi (círculo completo alrededor del eje z)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0 \leq \phi \leq \pi (desde el polo norte al polo sur)

La integral para el volumen es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} V &= \iiint_D dV \\ &= \int_0^{2\pi}\int_0^\pi\int_0^r \rho^2 \sin(\phi)\,d\rho\,d\phi\,d\theta \\ &= \int_0^{2\pi}d\theta \int_0^\pi \sin(\phi)\,d\phi \int_0^r \rho^2\,d\rho \\ &= (2\pi) (2) \left(\frac{r^3}{3}\right) \\ &= \frac{4}{3}\pi r^3 \end{align}

¡Y este es el volumen de una esfera! Las integrales múltiples son herramientas muy poderosas para calcular estas cantidades en matemáticas y ciencias.

Galería de imágenes

• 

  La integral doble como el volumen bajo una superficie. La región rectangular abajo de la figura es el dominio de integración, mientras que la superficie es la gráfica de la función de dos variables de la integral.

• 

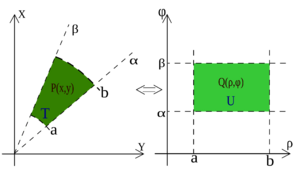
  La transformación de coordenadas rectangulares a polares. Se puede notar que el área de la región polar es distinta que la de la región rectangular, lo que justifica la necesidad del jacobiano. También se puede demostrar que si se considera 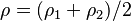(el radio medio), el área de la región polar es efectivamente .

• 

  Gráfica de las Coordenadas Cilíndricas (Se muestra el ángulo θ como φ)

• 

  Gráfica de las coordenadas esféricas

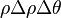Véase también

En inglés: Multiple integral Facts for Kids

• Integral
• Teorema de Green
• Teorema de Stokes
• Teorema de la divergencia
• Teorema de Fubini
• Integral de Riemann

Referencias

• Roland E. Larson, Robert P. Hosteler, Bruce H. Edwards (1999). «Integración Múltiple». Cálculo Volumen 2. México D.F.: McGrawHill. ISBN 970-10-2756-6. 
• Jerrold E. Marsden, Anthony J. Tromba (2004). Cálculo Vectorial. Quinta Edición. Pearson.

de:Integralrechnung#Mehrdimensionale Integration