Inmersión (matemática) para niños
En matemáticas, una inmersión es una forma especial de "dibujar" o "colocar" una forma geométrica (llamada variedad) dentro de otra más grande. Imagina que tienes una línea y la dibujas en una hoja de papel. Si la línea no tiene esquinas puntiagudas y no se "aplasta" en ningún punto, entonces es una inmersión. Aunque la línea se cruce a sí misma, si miras de cerca cualquier parte de ella, siempre parecerá una línea suave y continua.
La clave de una inmersión es que, en cada punto, la forma se estira o se dobla de manera suave, sin que ninguna parte se comprima hasta convertirse en un punto. Esto se describe con una idea matemática llamada "derivada inyectiva", que significa que no hay "aplastamiento" local.
Un concepto parecido es el de encaje. Un encaje es una inmersión que además no se cruza a sí misma en ningún lugar. Piensa en un encaje como si dibujaras una línea en el papel que nunca se toca ni se cruza. Si una forma es compacta (como un círculo, que no tiene "bordes" que se extienden infinitamente), una inmersión que no se cruza es siempre un encaje. Pero si la forma no es compacta (como una línea infinita), puede que no se cruce, pero aun así no sea un encaje.
Contenido
¿Qué es una homotopía regular?
Una homotopía regular es como una película que muestra cómo una inmersión se transforma suavemente en otra. Imagina que tienes una forma dibujada y quieres cambiarla a otra forma, pero siempre manteniendo la propiedad de ser una inmersión (sin esquinas puntiagudas ni aplastamientos). La homotopía regular es el proceso continuo de esa transformación. Es como si la forma se moviera y se deformara sin dejar de ser una inmersión en ningún momento.
¿Quién estudió las inmersiones?
Hassler Whitney fue un matemático muy importante que empezó a estudiar las inmersiones y las homotopías regulares en los años 1940. Él demostró que, bajo ciertas condiciones de tamaño, siempre es posible transformar una forma en una inmersión, e incluso en un encaje. Estos descubrimientos son conocidos como los teoremas de inmersión y encaje de Whitney.
Otros matemáticos como Stephen Smale y Morris Hirsch continuaron desarrollando estas ideas, clasificando las inmersiones y entendiendo mejor cómo se comportan. Un resultado famoso de esto es la "eversión de la esfera", que es la idea de "voltear" una esfera del revés sin hacer agujeros ni pliegues.
¿Por qué algunas formas no pueden ser inmersas de ciertas maneras?
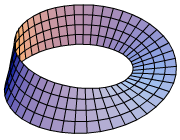
A veces, una forma no puede ser inmersa en un espacio de cierta manera debido a sus propiedades internas. Por ejemplo, la banda de Möbius es una superficie con una sola cara y un solo borde. No se puede "aplanar" completamente en un espacio de la misma dimensión sin que se cruce o se rompa de alguna manera. Esto se debe a una propiedad matemática llamada "fibrado normal estable", que es como una huella digital de la forma que indica cómo se puede doblar y estirar.
Véase también
 En inglés: Immersion (mathematics) Facts for Kids
En inglés: Immersion (mathematics) Facts for Kids
- Submersión
- Subvariedad inmersa
- Inmersión isométrica
- Teorema de inmersión de Nash


