Función gamma para niños

La función gamma (que se escribe como 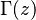, donde 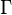es la letra griega gamma en mayúscula) es una herramienta matemática muy especial. Imagina que conoces el factorial de un número, como 5! (que es 5 x 4 x 3 x 2 x 1 = 120). El factorial solo funciona con números enteros positivos (0, 1, 2, 3...). La función gamma es como una versión extendida del factorial que puede usarse con números que no son enteros, ¡incluso con números complejos!

Fue el matemático Adrien-Marie Legendre quien propuso la forma en que se escribe esta función. La función gamma es muy útil en áreas como la probabilidad y la estadística, así como en la combinatoria, que es el estudio de cómo contar y organizar cosas.

¿Qué es la función gamma?

Función gamma en el eje real

El valor de la función gamma en el plano complejo

La función gamma se define con una fórmula matemática un poco compleja llamada integral. Si el número con el que trabajamos es positivo, esta integral funciona muy bien.

Una de las propiedades más importantes de la función gamma es que si tienes un número entero positivo n, la función gamma de n es igual al factorial de n-1. Es decir:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(n) = (n-1)!

Por ejemplo:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(1) = 0! = 1
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(2) = 1! = 1
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(3) = 2! = 2
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(4) = 3! = 6

Esto nos muestra cómo la función gamma se conecta directamente con el factorial.

¿Cómo se relaciona con el factorial?

La función gamma tiene una propiedad muy útil:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(z+1) = z \cdot \Gamma(z)

Esto significa que si conoces el valor de la función gamma para un número, puedes encontrar el valor para el siguiente número multiplicando por el número original.

Por ejemplo, si sabemos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(1) = 1 :

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(2) = 1 \cdot \Gamma(1) = 1 \cdot 1 = 1
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(3) = 2 \cdot \Gamma(2) = 2 \cdot 1 = 2
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(4) = 3 \cdot \Gamma(3) = 3 \cdot 2 = 6

¡Como ves, esto es exactamente igual que el factorial!

Propiedades interesantes

Gráfico del valor absoluto de la función gamma con argumento complejo

La función gamma tiene muchas propiedades especiales que la hacen muy útil en matemáticas avanzadas. Una de las más conocidas es que la función gamma de 1/2 es igual a la raíz cuadrada de pi:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma\left(\frac{1}{2}\right) = \sqrt{\pi}

Esto es un resultado sorprendente y muy importante en muchas áreas de la ciencia.

Valores especiales

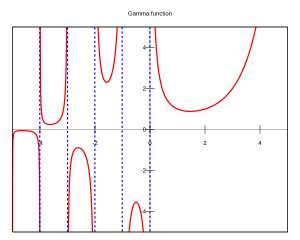
Aquí tienes algunos valores de la función gamma para que veas cómo se comporta:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma\left(-\frac{3}{2}\right) = \frac{4\sqrt{\pi}}{3} \approx 2.363
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma\left(-\frac{1}{2}\right) = -2\sqrt{\pi} \approx -3.545
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma\left(\frac{1}{2}\right) = \sqrt{\pi} \approx 1.772
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(1) = 1
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma\left(\frac{3}{2}\right) = \frac{\sqrt{\pi}}{2} \approx 0.886
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(2) = 1
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma\left(\frac{5}{2}\right) = \frac{3\sqrt{\pi}}{4} \approx 1.329
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(3) = 2
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma\left(\frac{7}{2}\right) = \frac{15\sqrt{\pi}}{8} \approx 3.323
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Gamma(4) = 6

¿Cómo se calcula?

Como la función gamma y el factorial crecen muy rápido, es difícil calcularlos para números muy grandes. Por eso, los matemáticos y los programas de computadora usan métodos especiales para aproximar sus valores. Algunas de estas formas son la fórmula de Stirling, la aproximación de Lanczos o la aproximación de Spouge.

Además, muchos programas de computadora calculan el logaritmo de la función gamma. El logaritmo crece más lentamente, lo que facilita los cálculos, especialmente cuando se trabaja con números muy grandes en problemas de combinatoria.

Aplicaciones de la función gamma

La función gamma tiene aplicaciones en muchas áreas, incluso en un campo llamado "cálculo fraccionario". Este campo explora la idea de derivadas e integrales de orden no entero.

Por ejemplo, si sabes cómo calcular la derivada de una expresión como 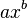(donde a y b son números), la función gamma permite calcular derivadas de "orden fraccionario", como la derivada de 1/2.

Así, se pueden calcular cosas como:

• La derivada de 1/2 de es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{2\sqrt{x}}{\sqrt{\pi}}
• La derivada de 1/2 de 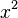es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{8\sqrt{x^{3}}}{3\sqrt{\pi}}
• La derivada de 1/2 de una constante c es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{c}{\sqrt{\pi}\sqrt{x}}

Esto demuestra lo versátil que es la función gamma en matemáticas avanzadas.

Véase también

En inglés: Gamma function Facts for Kids

• Función beta
• Factorial
• Distribución Gamma
• Fórmula de Stirling

Galería de imágenes

• 

  La función gamma en el plano complejo