Función contador de números primos para niños
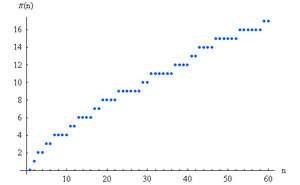
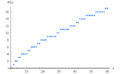
En matemática, la función contador de números primos es una herramienta especial que nos ayuda a saber cuántos números primos hay hasta un número determinado. Se escribe como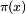 
(¡no la confundas con el famoso número π!) y nos dice cuántos números primos son menores o iguales a un número x.
Por ejemplo:
- π(1) = 0 (no hay primos menores o iguales a 1)
- π(2) = 1 (el único primo menor o igual a 2 es el 2)
- π(3) = 2 (los primos menores o iguales a 3 son el 2 y el 3)
- π(4) = 2 (siguen siendo el 2 y el 3)
- π(5) = 3 (los primos menores o iguales a 5 son el 2, el 3 y el 5)
- π(10) = 4 (los primos menores o iguales a 10 son el 2, el 3, el 5 y el 7)
Contenido
¿Qué es la función contador de números primos?
La función contador de números primos, representada como π(x), es como un "contador" de números primos. Un número primo es un número entero mayor que 1 que solo se puede dividir exactamente por 1 y por sí mismo (como 2, 3, 5, 7, 11, etc.).
Esta función nos da el total de números primos que existen desde el 2 hasta el número x que elijamos. Es muy útil en el estudio de los números y sus propiedades.
El Teorema de los Números Primos: Un Descubrimiento Fascinante
Uno de los resultados más importantes relacionados con la función π(x) es el llamado Teorema de los Números Primos. Este teorema nos dice que, cuando el número x es muy, muy grande, el valor de π(x) se parece mucho a la división de x entre el logaritmo natural de x (ln x).
Esto se escribe así:
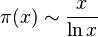
No significa que la diferencia entre ellos sea cero, sino que su relación se acerca a 1. Es decir, si dividimos π(x) entre x/ln x, el resultado se acerca a 1 a medida que x crece.
¿Quién descubrió el Teorema de los Números Primos?
La idea de esta aproximación fue propuesta por primera vez por el famoso matemático Carl Friedrich Gauss. Después de muchos intentos de otros matemáticos, Jacques Hadamard y Charles de la Vallée-Poussin lograron demostrar este teorema de forma independiente. Esto ocurrió a finales del siglo XIX.
¿Qué nos dice la densidad de números primos?
El Teorema de los Números Primos también nos ayuda a entender cómo se distribuyen los números primos. Si reescribimos la relación anterior como:
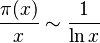
Podemos interpretar que la "densidad media" de números primos entre los números enteros se acerca a 1/lnx a medida que x se hace más grande. Esto significa que, a medida que exploramos números más grandes, los números primos se vuelven menos frecuentes, pero podemos predecir su aparición.
Mejorando la aproximación de Gauss
Unos 25 años después de que Gauss hiciera su descubrimiento, otro matemático, Adrien-Marie Legendre, encontró una forma aún más precisa de aproximar la función π(x):
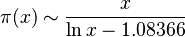
Esta fórmula es un poco más compleja, pero da un resultado más cercano al valor real de π(x) para números grandes.
Galería de imágenes
-
Los 60 primeros valores de π(n).
Véase también
En inglés: Prime-counting function Facts for Kids
