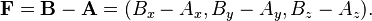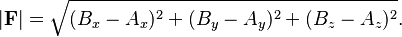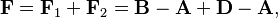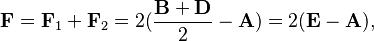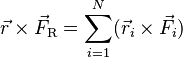Fuerza neta para niños

Enciclopedia para niños

La fuerza neta es como la fuerza total que actúa sobre un objeto. Imagina que varias personas empujan una caja en diferentes direcciones; la fuerza neta sería la fuerza única que representa el efecto combinado de todos esos empujones. Esta fuerza única le da al objeto la misma aceleración que si todas las fuerzas originales actuaran juntas, tal como lo explica la segunda ley de movimiento de Newton.

En física, la fuerza neta también puede tener un efecto de giro, llamado torque. Si un objeto puede girar, la fuerza neta, junto con su torque asociado, se convierte en la fuerza resultante. Esta fuerza resultante tiene el mismo efecto en el movimiento de rotación del objeto que todas las fuerzas reales combinadas. A veces, un conjunto de fuerzas puede tener una fuerza resultante que no produce ningún giro. En ese caso, la fuerza neta, aplicada en el lugar correcto, tiene el mismo efecto en el objeto que todas las fuerzas originales. Sin embargo, no siempre es posible encontrar una fuerza resultante que no cause giro.

Contenido

¿Qué es la fuerza total?
¿Cómo se suman las fuerzas con la regla del paralelogramo?
¿Cómo afectan las fuerzas al movimiento de un objeto?
- Fuerzas en un punto
- Cuerpos rígidos
¿Qué es la fuerza resultante?
¿Para qué se usa la fuerza neta?
Véase también
Referencias

¿Qué es la fuerza total?

Un dibujo que muestra cómo se suman las fuerzas.

Una fuerza es una cantidad vectorial. Esto significa que tiene dos características importantes: una magnitud (cuán grande es la fuerza) y una dirección (hacia dónde empuja o tira). Las fuerzas se suelen representar con una letra en negrita, como F, o con una flecha encima, como 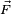$\scriptstyle \vec F$ .

En un dibujo, una fuerza se representa como una línea que va desde el punto donde se aplica (punto A) hasta otro punto (punto B). La dirección de la línea indica la dirección de la fuerza, y la longitud de la línea AB muestra la magnitud de la fuerza.

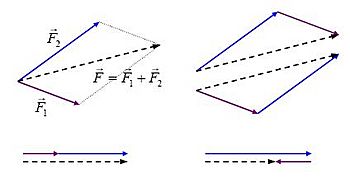
Aunque el cálculo vectorial es más moderno (finales del siglo XIX y principios del siglo XX), la regla del paralelogramo para sumar fuerzas se conoce desde hace mucho tiempo. Científicos como Galileo y Newton ya la usaban.

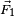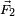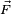El dibujo de al lado muestra cómo se suman dos fuerzas, $\scriptstyle \vec{F}_{1}$ y $\scriptstyle \vec{F}_{2}$ . La suma, $\scriptstyle \vec F$ , se dibuja como la diagonal de un paralelogramo que se forma con las dos fuerzas.

Cuando varias fuerzas actúan sobre un objeto grande, pueden aplicarse en diferentes puntos. Las fuerzas son como "vectores atados", lo que significa que solo se pueden sumar directamente si se aplican en el mismo punto. La fuerza neta que se obtiene de todas las fuerzas que actúan sobre un objeto no mantiene su movimiento original a menos que se aplique en el mismo punto y con el giro (torque) adecuado. La fuerza neta aplicada en un solo punto con el torque correcto se conoce como la fuerza y el torque resultantes.

¿Cómo se suman las fuerzas con la regla del paralelogramo?

Una fuerza es un vector que tiene dirección, magnitud y un punto de aplicación. Una forma sencilla de describir una fuerza es usando una línea que va de un punto A a un punto B. Si las coordenadas de estos puntos son A = (A_x, A_y, A_z) y B = (B_x, B_y, B_z), entonces el vector de fuerza aplicado en A se calcula como:

\mathbf{F}= \mathbf{B}-\mathbf{A} = (B_x-A_x, B_y-A_y, B_z-A_z).

La longitud de este vector B - A nos da la magnitud de la fuerza F, y se calcula así:

|\mathbf{F}| = \sqrt{(B_x-A_x)^2+(B_y-A_y)^2+(B_z-A_z)^2}.

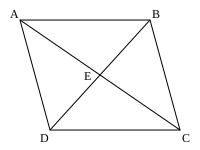
Para sumar dos fuerzas, F₁ y F₂, que se aplican en el mismo punto A, podemos sumar los segmentos que las representan. Si F₁ = B - A y F₂ = D - A, entonces la suma de estos dos vectores es:

\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2 = \mathbf{B}-\mathbf{A} + \mathbf{D}-\mathbf{A},

Esto también se puede escribir como:

\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2 = 2(\frac{\mathbf{B}+\mathbf{D}}{2}-\mathbf{A})=2(\mathbf{E}-\mathbf{A}),

Aquí, E es el punto medio del segmento BD que une los puntos B y D.

Así, la suma de las fuerzas F₁ y F₂ es el doble del segmento que une el punto A con el punto medio E del segmento que une los puntos finales B y D de las dos fuerzas. Para visualizar esto, se puede dibujar un segmento BC paralelo a AD y un segmento DC paralelo a AB, formando un paralelogramo ABCD. La diagonal AC de este paralelogramo es la suma de los dos vectores de fuerza. Esto se conoce como la regla del paralelogramo para la suma de fuerzas.

¿Cómo afectan las fuerzas al movimiento de un objeto?

Fuerzas en un punto

Cuando una fuerza actúa sobre una partícula (un objeto muy pequeño), se considera que se aplica en un solo punto. A esto se le llama fuerza puntual. Pero si la fuerza actúa sobre un objeto más grande, puede estar distribuida sobre una parte de su superficie o volumen. Para entender cómo esta fuerza hace girar el objeto, necesitamos saber dónde se aplica. Generalmente, esto se resuelve de dos maneras:

Si la zona donde actúa la fuerza es pequeña comparada con el tamaño del objeto, podemos imaginar que la fuerza actúa en un solo punto. Luego, se verifica si este "atajo" es lo suficientemente preciso.
Si no es preciso (por ejemplo, en el caso de la fuerza de gravedad), la fuerza distribuida se divide en muchas fuerzas pequeñas, cada una actuando sobre una partícula. Los cálculos se hacen para cada una, a menudo usando matemáticas avanzadas. Sin embargo, a veces se puede demostrar que todas esas fuerzas pequeñas pueden ser reemplazadas por una sola fuerza puntual sin necesidad de cálculos complejos (como ocurre con la fuerza de gravedad uniforme).

En resumen, el estudio del movimiento de un cuerpo rígido (un objeto que no se deforma) siempre empieza con el modelo de fuerza puntual. Cuando se dibuja una fuerza sobre un objeto, la línea que la representa suele empezar o terminar en el punto donde se aplica.

Cuerpos rígidos

Cómo una fuerza acelera un cuerpo.

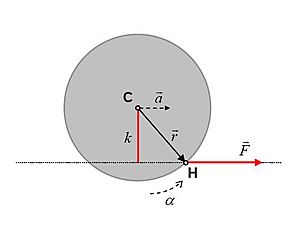
En el dibujo de al lado, una sola fuerza 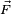$\scriptstyle \vec F$ actúa en el punto H sobre un objeto rígido que se mueve libremente. El objeto tiene una masa 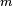$\scriptstyle m$ y su centro de masa es el punto C. Si la masa del objeto no cambia, la fuerza provoca cambios en su movimiento que se describen con estas expresiones:

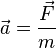\vec a = {\vec F \over m}

es la aceleración del centro de masa (el objeto se mueve en línea recta); y

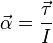\vec \alpha = {\vec \tau \over I}

es la aceleración angular del objeto (el objeto gira).

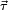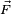En la segunda expresión, $\scriptstyle \vec \tau$ es el torque o momento de fuerza, y $\scriptstyle I$ es el momento de inercia del objeto (una medida de su resistencia a girar). El torque causado por una fuerza $\scriptstyle \vec F$ es una cantidad vectorial que se define con respecto a un punto de referencia:

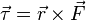\vec \tau = \vec r \times \vec F

es el vector de torque y

\ \tau = Fk

es la magnitud del torque

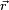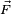El vector $\scriptstyle \vec r$ es el vector de posición del punto donde se aplica la fuerza, y en este ejemplo se dibuja desde el centro de masa (que es el punto de referencia). El segmento de línea recta $\scriptstyle k$ es el "brazo de palanca" de la fuerza $\scriptstyle \vec F$ con respecto al centro de masa. Como muestra el dibujo, el torque no cambia (el brazo de palanca es el mismo) si el punto de aplicación se mueve a lo largo de la línea de acción de la fuerza (la línea negra punteada). Esto significa que el efecto de giro de la fuerza solo depende de la posición de su línea de acción, no del punto exacto donde se aplica a lo largo de esa línea.

El vector de torque es perpendicular al plano formado por la fuerza y el vector 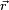$\scriptstyle \vec r$ . En este ejemplo, apunta hacia el observador. El vector de aceleración angular tiene la misma dirección. La regla de la mano derecha ayuda a relacionar esta dirección con el giro en sentido horario o antihorario en el plano del dibujo.

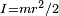El momento de inercia $\scriptstyle I$ se calcula con respecto a un eje que pasa por el centro de masa y es paralelo al torque. Si el objeto del dibujo es un disco uniforme, su momento de inercia es $\scriptstyle I=m r^2 /2$ . Por ejemplo, si el disco tiene una masa de 0,5 kg y un radio de 0,8 m, su momento de inercia es 0,16 kg m². Si la fuerza es de 2 N y el brazo de palanca es de 0,6 m, el torque es de 1,2 Nm. En el instante mostrado, la fuerza le da al disco una aceleración angular α = $τ$ / I = 7,5 rad/s², y a su centro de masa le da una aceleración lineal = F/m = 4 m/s².

¿Qué es la fuerza resultante?

Cómo se coloca gráficamente la fuerza resultante.

La fuerza resultante y el torque reemplazan los efectos de un conjunto de fuerzas que actúan sobre el movimiento de un objeto rígido. Un caso especial interesante es cuando la fuerza resultante no produce torque, y se puede encontrar de la siguiente manera:

Se usa la suma de vectores para encontrar la fuerza neta.
Se usa una ecuación para encontrar el punto de aplicación donde el torque es cero:

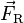\vec r \times \vec F_\mathrm{R} = \sum_{i=1}^N ( \vec r_i \times \vec F_i )

Donde $\vec F_\mathrm{R}$ es la fuerza neta, 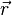$\vec r$ es su punto de aplicación, y 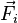$\vec F_i$ son las fuerzas individuales con sus puntos de aplicación 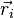$\vec r_i$ . A veces, no hay un punto de aplicación que haga que el torque sea cero.

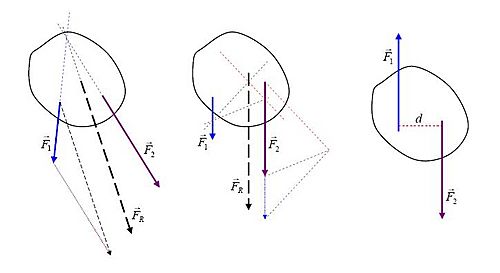
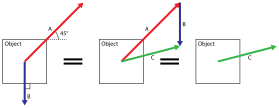
El dibujo de al lado muestra métodos gráficos sencillos para encontrar la línea de acción de la fuerza resultante en sistemas simples:

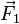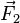Líneas de acción de las fuerzas reales. Las fuerzas $\vec{F}_{1}$ y $\vec{F}_{2}$ en el dibujo de la izquierda se cruzan. Después de sumar los vectores, la fuerza neta se mueve para que su línea de acción pase por el punto donde se cruzan las fuerzas originales. Con respecto a ese punto, todos los torques son cero, por lo que el torque de la fuerza resultante 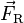$\vec{F}_\mathrm{R}$ es igual a la suma de los torques de las fuerzas reales.
El dibujo del medio muestra dos fuerzas reales paralelas. Después de sumar los vectores, la fuerza neta se mueve a la línea de acción correcta, donde se convierte en la fuerza resultante 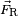$\scriptstyle \vec{F}_\mathrm{R}$ . Este proceso se basa en dividir todas las fuerzas en componentes cuyas líneas de acción se cruzan en un punto (llamado polo, que se elige libremente). Luego, se aplican los mismos principios del caso anterior para entender las relaciones de torque.
El dibujo de la derecha muestra un par de fuerzas, que son dos fuerzas iguales pero en direcciones opuestas. La fuerza neta es cero, pero producen un torque neto 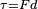$\scriptstyle \tau = Fd$ , donde $\scriptstyle \ d$ es la distancia entre sus líneas de acción. Como no hay una fuerza resultante, este torque se describe como un torque "puro".

¿Para qué se usa la fuerza neta?

Diagrama vectorial para la suma de fuerzas no paralelas.

En general, un conjunto de fuerzas que actúan sobre un objeto rígido siempre se puede reemplazar por una fuerza más un torque puro. La fuerza es la fuerza neta, pero para calcular el torque adicional, se debe elegir una línea de acción para la fuerza neta. Esta línea de acción se puede elegir libremente, pero el torque puro adicional dependerá de esa elección. En un caso especial, es posible encontrar una línea de acción donde este torque adicional sea cero.

La fuerza y el torque resultantes se pueden determinar para cualquier combinación de fuerzas. Sin embargo, un caso especial muy útil es cuando la fuerza resultante no produce torque. Esto es importante, tanto para entender como para aplicar, porque el objeto se mueve sin girar, como si fuera una partícula.

Algunos expertos no hacen distinción entre la fuerza resultante y la fuerza neta, y usan los términos como sinónimos.

Véase también

En inglés: Resultant force Facts for Kids

Teoría del tornillo
Centro de masa
Centros de gravedad en campos no uniformes

Referencias

Obtenido de «https://ninos.kiddle.co/index.php?title=Fuerza_neta&oldid=4761886»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Fuerza neta para Niños. Enciclopedia Kiddle.