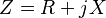Impedancia para niños
La impedancia es una medida de la oposición que un circuito eléctrico presenta al paso de la corriente cuando se le aplica un voltaje. Imagina que la corriente eléctrica es como el agua que fluye por una tubería. La resistencia sería como una parte estrecha de la tubería que dificulta el paso del agua. La impedancia es un concepto más amplio que incluye esta "resistencia" y otras oposiciones que aparecen, especialmente en circuitos de corriente alterna (CA).
En los circuitos de corriente continua (CC), la impedancia es igual a la resistencia. Pero en los circuitos de CA, la impedancia no solo tiene un valor (magnitud), sino también una "dirección" o "fase", que indica cómo se adelanta o atrasa la corriente respecto al voltaje.
La impedancia se calcula dividiendo el voltaje entre la corriente. Se representa con la letra Z.
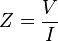
Donde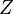 
es la impedancia, 
es el voltaje e 
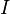es la corriente.
El concepto de impedancia es muy importante cuando la corriente cambia con el tiempo, como en la corriente alterna. La impedancia se compone de dos partes: la parte real, que es la resistencia, y la parte imaginaria, que se llama reactancia.
La impedancia nos permite usar una versión de la ley de Ohm para circuitos de corriente alterna, conocida como la ley de Ohm de corriente alterna:
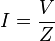
El término "impedancia" fue creado por Oliver Heaviside en 1886.
Contenido
¿Qué es la impedancia y cómo se define?
La impedancia es una forma de describir cómo un componente o un circuito se opone al flujo de corriente alterna. Se usa un tipo especial de número, llamado número complejo, para representarla.
La impedancia como número complejo
Cuando un circuito es alimentado por una corriente que cambia de forma sinusoidal (como una onda), el voltaje entre sus extremos también cambia de forma sinusoidal. La impedancia se define como un número complejo que tiene dos partes:
- Su magnitud (o módulo) es la relación entre el valor máximo del voltaje y el valor máximo de la corriente.
- Su argumento (o fase) es el ángulo que indica cuánto se adelanta o atrasa el voltaje con respecto a la corriente.
La impedancia se puede escribir de varias maneras, pero una forma común es:
Aquí,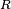 
es la parte resistiva (la resistencia normal) y 
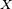es la parte reactiva (la reactancia). La letra Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \scriptstyle{j} se usa para indicar la parte imaginaria, para no confundirla con la letra Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \scriptstyle{i} que a veces se usa para la corriente.
Hay dos tipos principales de reactancia:
- Reactancia inductiva (
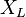): Es la oposición al cambio de corriente causada por componentes llamados inductores (como bobinas). - Reactancia capacitiva (
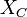): Es la oposición al cambio de voltaje causada por componentes llamados capacitores (o condensadores).
¿Qué es la admitancia?
La admitancia es lo contrario de la impedancia. Si la impedancia mide la oposición, la admitancia mide la facilidad con la que la corriente fluye a través de un circuito. Se representa con la letra Y.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Y= \textstyle{1\over Z}
La unidad de la admitancia es el siemens (S), que es el inverso del ohmio (la unidad de resistencia).
¿Cómo se representa la impedancia gráficamente?
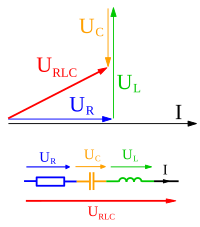
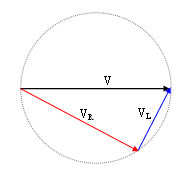
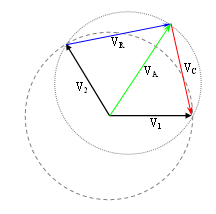
Podemos dibujar las tensiones y corrientes en un plano complejo como si fueran flechas que giran. Estas flechas se llaman fasores. La longitud de la flecha representa la magnitud del voltaje o la corriente, y el ángulo de la flecha con respecto a un eje nos muestra su fase. Este tipo de dibujo se conoce como diagrama de Fresnel.
Estos diagramas nos ayudan a "ver" cómo se suman las tensiones y corrientes en un circuito, haciendo más fácil entender su comportamiento.
Cálculo de circuitos con impedancias
Usar impedancias simplifica mucho el cálculo de circuitos que tienen resistencias, inductores y condensadores. Sin embargo, estas reglas solo funcionan bajo ciertas condiciones:
- Cuando el circuito está en un estado estable con corriente alterna sinusoidal. Esto significa que todas las fuentes de voltaje y corriente son ondas suaves y constantes, y que cualquier cambio brusco ya ha terminado.
- Cuando todos los componentes son lineales. Esto significa que la corriente es directamente proporcional al voltaje aplicado. No se pueden usar con componentes no lineales como los diodos.
¿Cómo se aplican las leyes de Kirchhoff?
Las leyes de Kirchhoff se usan de la misma manera que en los circuitos de corriente continua:
- La suma de las corrientes que llegan a un punto (nodo) es cero.
- La suma de todos los voltajes alrededor de un camino cerrado (malla) es cero.
La diferencia es que, en este caso, las corrientes y voltajes son números complejos.
¿Cómo se generaliza la ley de Ohm?
El voltaje entre los extremos de una impedancia es igual al producto de la corriente por la impedancia:
Tanto la impedancia, como la corriente y el voltaje son, en general, números complejos.
¿Cómo se combinan las impedancias en serie o en paralelo?
Las impedancias se combinan de forma similar a las resistencias:
- En serie: La impedancia total es la suma de las impedancias individuales.
:Serie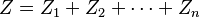 
- En paralelo: La impedancia total es el inverso de la suma de los inversos de cada impedancia.
:Paralelo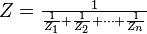 
Ejemplos de impedancia en componentes básicos
La impedancia de cada tipo de componente es diferente:
- Resistencia: La impedancia de una resistencia ideal es simplemente su valor de resistencia (
). Aquí, el voltaje y la corriente están en fase, es decir, no hay adelanto ni atraso.
- Inductor: La impedancia de un inductor ideal aumenta a medida que la frecuencia de la corriente alterna es mayor.
:
Donde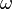 
es la frecuencia angular y 
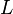es la inductancia.
- Condensador: La impedancia de un condensador ideal disminuye a medida que la frecuencia de la corriente alterna es mayor.
:
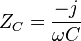Donde 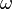es la frecuencia angular y 
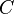es la capacitancia.
Ejemplo con un solo generador
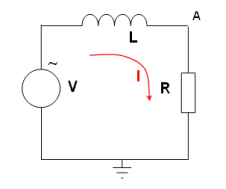
Imaginemos un circuito con un generador de voltaje sinusoidal, una bobina (inductor) y una resistencia, todos conectados en serie.
Si el generador tiene un voltaje de 10 voltios de amplitud y una frecuencia de 10 kHz, y la bobina es de 10 mH y la resistencia de 1,2 kΩ, podemos calcular la corriente que circula.
Usando las fórmulas de impedancia para la bobina y la resistencia, y luego la ley de Ohm generalizada, obtenemos la corriente. El resultado será un número complejo.
Por ejemplo, el valor de la corriente (su magnitud) sería de aproximadamente 7,38 miliamperios (mA) en su punto máximo. La fase de la corriente nos diría que está un poco atrasada con respecto al voltaje del generador, lo cual es normal en un circuito con una bobina.
En este tipo de circuitos, solo la resistencia consume energía. La bobina y el condensador almacenan y liberan energía, pero no la disipan.
Es importante recordar que cuando sumamos voltajes en un circuito de corriente alterna, no podemos simplemente sumar los valores que leeríamos con un voltímetro. Necesitamos sumar los fasores (los números complejos) porque tienen una fase o "dirección" que también importa.
Ejemplo con dos generadores desfasados
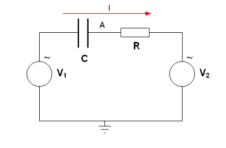
Consideremos un circuito con un condensador y una resistencia en serie, conectados entre dos generadores de voltaje sinusoidal que están desfasados (uno empieza un poco después que el otro).
Si los generadores son como los de un sistema eléctrico trifásico, uno podría ser nuestra referencia y el otro estaría adelantado en fase.
Calculando la diferencia de voltaje entre los dos generadores usando números complejos, podemos encontrar la corriente que circula por el circuito. Esta corriente también tendrá una magnitud y una fase.
De nuevo, la suma de los voltajes medidos con un voltímetro en cada componente (resistencia y condensador) podría ser mayor que el voltaje total aplicado por los generadores. Esto se debe a que los voltajes no están en fase y no se suman directamente como números simples.
Galería de imágenes
-
Impedancia línea bifiliar
Véase también
En inglés: Electrical impedance Facts for Kids
