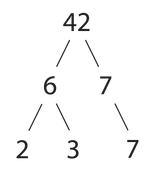
Factorización de enteros para niños
La factorización de enteros es como un juego de rompecabezas con números. Consiste en tomar un número grande y "descomponerlo" en números más pequeños que, al multiplicarse, te dan el número original. Imagina que tienes un número como el 12. Puedes descomponerlo en 2 x 6, o 3 x 4. Si sigues descomponiendo hasta que todos los números sean primos (números que solo se pueden dividir por 1 y por sí mismos, como 2, 3, 5, 7...), entonces tienes la factorización en primos. Por ejemplo, el 12 se descompone en 2 x 2 x 3.
Cuando los números son muy, muy grandes, encontrar estos "pedacitos" primos es increíblemente difícil para las computadoras actuales. Es tan difícil que se usa como base para proteger información importante en internet, como tus mensajes o tus datos bancarios. Esto se llama criptografía. Un ejemplo famoso es el sistema RSA, que se basa en que es casi imposible descomponer números gigantes en sus factores primos.
Muchos expertos en matemáticas y computación, en áreas como la teoría algebraica de números o la computación cuántica, estudian este problema para encontrar formas más rápidas de resolverlo o para entender mejor sus secretos.
Los casos más difíciles de factorizar son cuando el número grande es el resultado de multiplicar dos números primos muy grandes y de tamaño parecido.
Contenido
¿Qué es la Descomposición en Factores Primos?
Una idea muy importante en matemáticas, llamada el teorema fundamental de la aritmética, dice que cada número entero positivo (mayor que cero) tiene una única forma de descomponerse en números primos. Es como si cada número tuviera su propia "receta" secreta hecha solo con ingredientes primos.
La mayoría de los métodos para factorizar números son de "propósito general". Esto significa que sirven para descomponer cualquier número que les des. La única diferencia entre ellos es cuánto tiempo tardan en darte el resultado.
Por ejemplo, para descomponer el número 72 en sus factores primos, podemos hacer esto:
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{r|l} 72 & 2 \\ 36 & 2 \\ 18 & 2 \\ 9 & 3 \\ 3 & 3 \\ 1 & \end{array} |
| Esto significa que 72 es igual a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 \times 2 \times 2 \times 3 \times 3 , o de forma más corta: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 72 = 2^3 \cdot 3^2 \, |
Factorización y Computadoras Cuánticas
Hasta ahora, las computadoras normales no pueden factorizar números grandes de forma rápida. Si alguien encontrara una manera de hacerlo, sería una noticia enorme en el mundo de la criptografía, porque muchos sistemas de seguridad que usamos hoy dejarían de ser seguros.
Sin embargo, existe un tipo especial de computadora, llamada computación cuántica, que podría cambiar esto. Un científico llamado Peter Shor creó un algoritmo (una serie de pasos para resolver un problema) que permite a una computadora cuántica factorizar números primos muy rápido. Este descubrimiento hizo que mucha gente se interesara en las computadoras cuánticas.
Ya se han construido algunas computadoras cuánticas pequeñas que pueden factorizar números pequeños. Se espera que, con los avances tecnológicos, estas computadoras puedan algún día factorizar números tan grandes que podrían poner en riesgo los sistemas de seguridad actuales.
¿Para qué sirve la dificultad de factorizar?
La dificultad de factorizar números grandes es el corazón de varios sistemas de seguridad importantes. Por ejemplo, el algoritmo RSA, que se usa para proteger mucha información en internet, se basa en que es muy difícil descomponer números grandes. Si se pudiera factorizar rápido, el sistema RSA ya no sería seguro.
Otros sistemas de seguridad, como el criptosistema Rabin o el generador de números pseudoaleatorios Blum Blum Shub, también dependen de esta dificultad. Si alguien encontrara una forma de "romperlos", también podría usar ese método para factorizar números más rápido.
Avances Recientes en Factorización
Un equipo de la Agencia Federal Alemana para Seguridad de Tecnología de Información (BSI) tiene el récord de haber factorizado números muy grandes. En 2005, lograron factorizar un número llamado RSA-200, que tenía 663 bits (una medida de su tamaño). Usaron un método llamado la criba general del cuerpo de números.
Ese mismo equipo también factorizó el RSA-640, un número un poco más pequeño, con 193 dígitos, en el mismo año.
Ambas factorizaciones necesitaron muchos meses de trabajo de computadoras, usando la potencia combinada de 80 procesadores Opteron de AMD. Esto demuestra lo difícil que es este problema para las computadoras actuales.
¿Qué tan difícil es realmente?
Si un número grande es el resultado de multiplicar dos números primos de tamaño similar, no existe un método conocido que pueda factorizarlo rápidamente en una computadora normal. Los mejores métodos actuales son muy lentos para números gigantes.
Sin embargo, para una computadora cuántica, el algoritmo de Shor (descubierto en 1994) sí puede resolverlo rápidamente. En 2001, una computadora cuántica de 7 "qubits" (las unidades básicas de información cuántica) fue la primera en usar el algoritmo de Shor para factorizar el número 15.
Es interesante notar que saber si un número es primo o no (lo que se llama "prueba de primalidad") es mucho más fácil que encontrar sus factores primos. Existen métodos muy rápidos para saber si un número es primo, incluso si es muy grande. Esta facilidad para probar la primalidad es clave para el funcionamiento del algoritmo RSA, ya que se necesitan números primos grandes para crearlo.
Métodos de Factorización
Existen diferentes métodos o algoritmos para factorizar números. Algunos son de "propósito general" y otros de "propósito específico".
Métodos de Propósito General
Estos métodos funcionan para cualquier número y su velocidad depende del tamaño del número. Son los que se usan para factorizar los números grandes de los sistemas de seguridad como RSA. Algunos ejemplos son:
- Criba cuadrática
- Algoritmo general de criba del cuerpo de números
Métodos de Propósito Específico
La velocidad de estos métodos depende de las características de los factores que se buscan (por ejemplo, si son pequeños o tienen una forma especial). Algunos ejemplos son:
- División por tentativa (el método más simple, probando dividir por números pequeños)
- Algoritmo rho de Pollard
- Factorización de curva elíptica de Lenstra
- Método de factorización de Fermat
Otros Métodos Importantes
- Algoritmo de Shor, que es especial para computadoras cuánticas.
Véase también
 En inglés: Integer factorization Facts for Kids
En inglés: Integer factorization Facts for Kids
- Tabla de factores primos


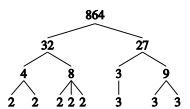
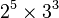 .
.