Factor de Lorentz para niños
El factor de Lorentz (también conocido como factor gamma) es un número muy importante en la teoría especial de la relatividad. Esta teoría, creada por Albert Einstein, nos ayuda a entender cómo se comportan el tiempo y el espacio cuando los objetos se mueven a velocidades muy, muy altas, cercanas a la velocidad de la luz.
El factor de Lorentz se representa con la letra griega gamma (γ). Aparece en muchas fórmulas de la relatividad. Nos ayuda a calcular cómo cambian cosas como el tiempo o la longitud de un objeto cuando se mueve muy rápido. Su nombre se debe a Hendrik Lorentz, un científico que lo usó por primera vez en sus estudios sobre la electricidad y el magnetismo.
Contenido
¿Qué es el Factor de Lorentz?
El factor de Lorentz es un número que nos dice cuánto se "estiran" o "encogen" el tiempo y el espacio cuando un objeto se mueve a una velocidad considerable. Imagina que viajas en una nave espacial a una velocidad cercana a la de la luz. Para ti, el tiempo pasaría de forma normal. Pero para alguien que te observa desde la Tierra, tu tiempo parecería ir más lento. Este cambio se calcula usando el factor de Lorentz.
¿Para qué se usa el Factor de Lorentz?
Este factor es clave para entender varios fenómenos sorprendentes de la relatividad:
- Dilatación del tiempo: El tiempo pasa más lento para un objeto que se mueve muy rápido en comparación con uno que está quieto.
- Contracción de longitudes: Un objeto que se mueve muy rápido parece más corto en la dirección de su movimiento para un observador que está quieto.
- También se usa en las fórmulas para calcular la energía cinética (la energía del movimiento) y el momento lineal (la cantidad de movimiento) de objetos que se mueven a altas velocidades.
¿Cómo se calcula el Factor de Lorentz?
El factor de Lorentz se calcula con una fórmula que incluye la velocidad del objeto y la velocidad de la luz. La fórmula principal es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}
Donde:
- γ es el factor de Lorentz.
- v es la velocidad del objeto que se está moviendo.
- c es la velocidad de la luz en el vacío (aproximadamente 300,000 kilómetros por segundo).
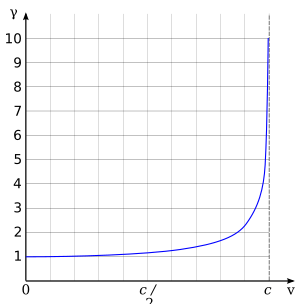
La parte Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{v}{c} se llama beta (β) y representa la velocidad del objeto comparada con la velocidad de la luz. Si un objeto está quieto (v=0), el factor de Lorentz es 1. Esto significa que no hay cambios en el tiempo ni en la longitud. Pero a medida que la velocidad (v) se acerca a la velocidad de la luz (c), el factor de Lorentz se hace cada vez más grande.
Valores del Factor de Lorentz según la velocidad
Aquí puedes ver cómo cambia el factor de Lorentz a diferentes velocidades:
| Velocidad relativa (v/c) | Factor de Lorentz (γ) |
|---|---|
| 0% (objeto quieto) | 1.0000 |
| 10% de la velocidad de la luz | 1.0050 |
| 50% de la velocidad de la luz | 1.1547 |
| 80% de la velocidad de la luz | 1.6667 |
| 90% de la velocidad de la luz | 2.2942 |
| 99% de la velocidad de la luz | 7.0888 |
| 99.9% de la velocidad de la luz | 22.3663 |
Como puedes ver en la tabla, cuando la velocidad es baja, el factor de Lorentz es muy cercano a 1. Esto significa que los efectos de la relatividad son tan pequeños que no los notamos en nuestra vida diaria. Pero a velocidades muy altas, el factor de Lorentz aumenta mucho, y los efectos se vuelven muy importantes.
¿Cómo se descubrió el Factor de Lorentz?
La idea del factor de Lorentz surgió de la observación de que la velocidad de la luz es siempre la misma para cualquier observador, sin importar cómo se esté moviendo ese observador.
Imagina a dos personas:
- Una persona A está en una nave espacial que se mueve muy rápido.
- Otra persona B está quieta en la Tierra.
Si la persona A en la nave enciende un láser que apunta hacia arriba, perpendicular a la dirección de su movimiento. Para la persona A, la luz sube en línea recta.
Pero para la persona B en la Tierra, que ve la nave moverse, el rayo de luz no sube en línea recta. Parece que la luz viaja en diagonal, porque la nave también se está moviendo hacia adelante mientras la luz sube.
Los científicos usaron el teorema de Pitágoras (el de los triángulos rectángulos) para calcular la distancia que recorre la luz vista por B. Al comparar el tiempo que tarda la luz en recorrer esa distancia para A y para B, se dieron cuenta de que el tiempo no pasaba igual para ambos. De esta comparación, se obtuvo la fórmula del factor de Lorentz, que explica esta diferencia en el paso del tiempo.
Véase también
 En inglés: Lorentz factor Facts for Kids
En inglés: Lorentz factor Facts for Kids