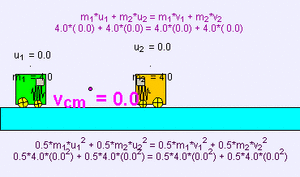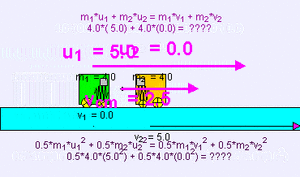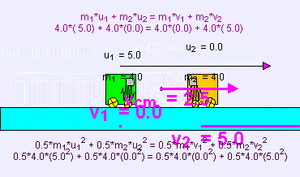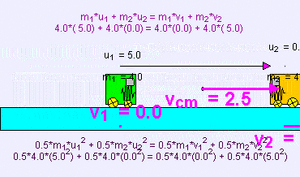Cantidad de movimiento para niños
La cantidad de movimiento, también conocida como momento lineal o ímpetu, es una medida que nos ayuda a entender el movimiento de un objeto. Imagina que un objeto se mueve: su cantidad de movimiento nos dice cuánto "empuje" o "fuerza de movimiento" tiene.
En la física clásica, la cantidad de movimiento se calcula multiplicando la masa de un objeto (cuánto material tiene) por su velocidad (qué tan rápido se mueve y en qué dirección). Es como si un objeto más pesado o uno que se mueve más rápido tuviera más "poder" en su movimiento.
Este concepto es muy importante en la física y fue estudiado por grandes científicos como Galileo Galilei e Isaac Newton. Ellos se dieron cuenta de que no solo la velocidad importa, sino también la masa del objeto.
Contenido
¿Qué es la Cantidad de Movimiento?
La cantidad de movimiento es una magnitud física que tiene dirección, como la velocidad. Se representa con la letra p. Para calcularla en la física más común (la mecánica newtoniana), usamos una fórmula sencilla:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{p} = m \cdot \mathbf{v}
Aquí, p es la cantidad de movimiento, m es la masa del objeto (medida en kilogramos, kg) y v es su velocidad (medida en metros por segundo, m/s).
¿Por qué es importante la masa?
Piensa en una mosca y un camión. Si ambos se mueven a la misma velocidad, por ejemplo, a 40 kilómetros por hora, ¿cuál es más difícil de detener? ¡El camión, por supuesto! Esto se debe a que el camión tiene mucha más masa que la mosca. Aunque su velocidad sea la misma, el camión tiene una cantidad de movimiento mucho mayor. Esta idea nos ayuda a entender por qué la masa es tan importante al describir el movimiento.
La Cantidad de Movimiento y las Leyes de Newton
La cantidad de movimiento está muy relacionada con las leyes de Newton sobre el movimiento. De hecho, la famosa Segunda ley de Newton (Fuerza = masa x aceleración) se puede entender mejor si pensamos en la cantidad de movimiento. La fuerza que actúa sobre un objeto es igual a cómo cambia su cantidad de movimiento con el tiempo.
¿Cómo se conserva la Cantidad de Movimiento?
Una de las cosas más fascinantes de la cantidad de movimiento es que obedece a una ley de conservación. Esto significa que en un sistema cerrado (donde no hay fuerzas externas actuando sobre él), la cantidad total de movimiento siempre se mantiene igual. ¡No se crea ni se destruye!
¿Qué significa "sistema cerrado"?
Un sistema cerrado es como una caja donde solo interactúan los objetos que están dentro. Si no hay nada de fuera que los empuje o los frene, la cantidad de movimiento total de todos los objetos dentro de la caja antes de una interacción (como un choque) será la misma que después de la interacción.
Por ejemplo, si dos bolas de billar chocan, la suma de sus cantidades de movimiento antes del choque es igual a la suma de sus cantidades de movimiento después del choque. La cantidad de movimiento se transfiere de una bola a otra, pero la cantidad total en el sistema de las dos bolas no cambia.
Cantidad de Movimiento en otros campos de la Física
Aunque la definición de la cantidad de movimiento como "masa por velocidad" es la más común y fácil de entender, en otras áreas de la física más avanzadas, como la teoría de la relatividad o la mecánica cuántica, el concepto se vuelve un poco más complejo.
- En la teoría de la relatividad, que estudia objetos que se mueven a velocidades cercanas a la de la luz, la cantidad de movimiento se calcula de una manera especial porque la masa de un objeto parece aumentar a medida que se acerca a la velocidad de la luz. Además, incluso cosas sin masa, como los fotones (partículas de luz), pueden tener cantidad de movimiento.
- En la mecánica cuántica, que estudia el mundo de las partículas muy pequeñas (como los átomos y electrones), la cantidad de movimiento se describe de una forma aún más abstracta, usando herramientas matemáticas avanzadas.
A pesar de estas diferencias, la idea principal de que la cantidad de movimiento es una propiedad fundamental del movimiento y que se conserva en sistemas cerrados, sigue siendo válida en todas las ramas de la física.
Galería de imágenes
-
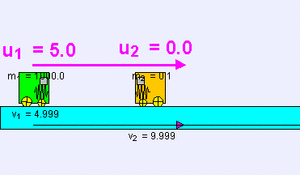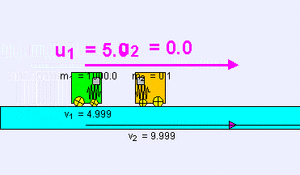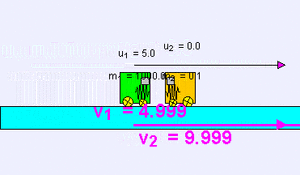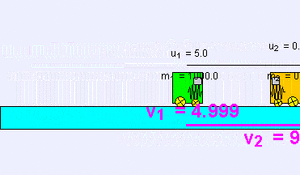
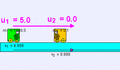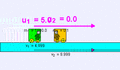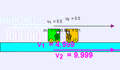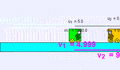
Ejemplo de colisión elástica (m1 = 1000 kg, u1 = 5 m/s, m2 = 0,1 kg, u2 = 0 m/s) de un objeto muy pesado contra otro muy ligero; existe una pequeña transferencia de momento al más ligero que sale disparado a mayor velocidad, mientras que el primer cuerpo apenas sufre una ligera deceleración v1 = 4,999 m/s, v2 = 9,999 m/s.
Véase también
 En inglés: Momentum Facts for Kids
En inglés: Momentum Facts for Kids
- Choque
- Impulso
- Leyes de Newton
- Velocidad