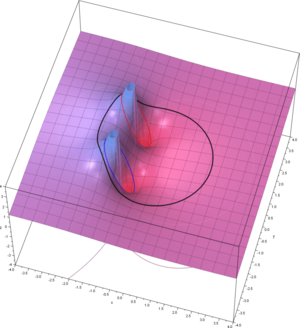
Fórmula integral de Cauchy para niños
La fórmula integral de Cauchy es una idea muy importante en las matemáticas, especialmente en una rama llamada análisis complejo. Lleva el nombre de un famoso matemático francés, Augustin Louis Cauchy.
Esta fórmula nos dice que si tienes una función especial (que es muy "suave" y se comporta bien) definida en un círculo, puedes saber todo sobre esa función dentro del círculo con solo conocer sus valores en el borde de ese círculo. Además, la fórmula te da maneras de calcular todas las derivadas de esa función usando integrales.
Una de las cosas más sorprendentes de la fórmula de Cauchy es que en el análisis complejo, "derivar es como integrar". Esto significa que las funciones complejas se comportan de una manera muy ordenada cuando se les aplican límites, algo que no siempre ocurre con las funciones en el análisis real (los números que usamos normalmente).
Contenido
¿Qué dice el Teorema de la Fórmula Integral de Cauchy?
Imagina que tienes un área abierta en el plano complejo (un tipo de plano donde los números tienen una parte real y una parte imaginaria). Dentro de esa área, hay un círculo cerrado.
Si tienes una función especial, llamada función holomorfa, que funciona en esa área, y tomas el borde de ese círculo (como un camino que recorres en sentido contrario a las agujas del reloj), entonces para cualquier punto dentro del círculo, la fórmula te permite calcular el valor de la función en ese punto.
La fórmula se ve así: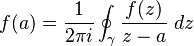 
Esta es la famosa fórmula integral de Cauchy. Para entenderla, necesitas saber que la función 
debe ser "diferenciable" en el plano complejo.
¿Por qué es tan importante esta fórmula?
La fórmula integral de Cauchy tiene muchas aplicaciones y nos enseña cosas muy interesantes sobre las funciones holomorfas:
Las funciones holomorfas son muy "suaves"
Gracias a esta fórmula, sabemos que una función que es holomorfa en un área abierta es en realidad infinitamente diferenciable. Esto significa que puedes calcular sus derivadas una y otra vez, ¡sin parar! En el mundo de los números reales, esto no siempre es cierto; una función puede tener una primera derivada, pero no una segunda, o una tercera, etc.
Las funciones holomorfas son "analíticas"
La fórmula también nos dice que toda función holomorfa es una función analítica. Esto significa que se puede representar como una serie de potencias, que es como una suma infinita de términos con potencias de una variable (por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + x^2 + x^3 + ... ). Esto es muy útil para entender cómo se comportan estas funciones.
Otras aplicaciones importantes
La fórmula de Cauchy también se usa para demostrar otros teoremas importantes en matemáticas, como:
- El teorema de los residuos, que ayuda a calcular integrales de funciones más complejas.
- El principio del argumento.
- El teorema de Morera, que dice que si tienes una secuencia de funciones holomorfas que se acercan mucho entre sí (convergen uniformemente), el resultado también será una función holomorfa.
El Teorema del Valor Medio de Gauss
Otra consecuencia de la fórmula es el Teorema del Valor Medio de Gauss. Este teorema dice que el valor de una función holomorfa en el centro de un círculo es igual al promedio de los valores de la función en todo el borde de ese círculo. Es como si el valor central fuera el "promedio" de lo que ocurre a su alrededor.
Ejemplo sencillo de aplicación
Vamos a ver un ejemplo de cómo se usa la fórmula. Imagina que tenemos una función como esta: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(z)=\frac{z^2}{z^2+2z+2} Y queremos calcular su integral alrededor de un círculo de radio 2.
Primero, necesitamos encontrar los puntos donde la función se vuelve "singular" (donde el denominador es cero y la función no está definida). Para nuestra función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(z) , estos puntos son Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z_1 = -1 + i y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z_2 = -1 - i . Ambos puntos están dentro de nuestro círculo de radio 2.
La fórmula de Cauchy nos permite dividir la integral grande en integrales más pequeñas alrededor de cada uno de estos puntos singulares. Al aplicar la fórmula cuidadosamente a cada parte, podemos sumar los resultados para obtener la integral total.
Por ejemplo, para el punto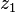 
, podemos reescribir la función de una manera que se ajuste a la fórmula de Cauchy y calcular la integral alrededor de un pequeño círculo que rodea solo a 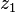. Hacemos lo mismo para 
.
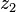Al final, sumando los resultados de estas dos integrales más pequeñas, obtenemos el valor de la integral original. En este caso, el resultado es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -4\pi i .
Generalizaciones de la fórmula
La fórmula integral de Cauchy es tan poderosa que se ha extendido a otras áreas de las matemáticas:
Funciones suaves
Existe una versión de la fórmula para funciones que son "suaves" (que tienen derivadas continuas), incluso si no son holomorfas. Esta versión se llama fórmula de Cauchy-Pompeiu y se basa en un teorema más general llamado teorema de Stokes.
Varias variables
La fórmula también se puede generalizar para funciones que dependen de varias variables complejas, no solo una. Esto es útil en campos más avanzados de las matemáticas.
En álgebras reales
Incluso en espacios reales con más de dos dimensiones, la idea de la fórmula integral de Cauchy se puede aplicar usando un concepto matemático llamado álgebra geométrica. Esto nos permite entender cómo se relacionan las funciones y sus derivadas en espacios más complejos.
Véase también
En inglés: Cauchy's integral formula Facts for Kids
- Teorema integral de Cauchy
- Ecuaciones de Cauchy-Riemann
- Teorema de Morera
- Función de Green
- Fórmula integral de Schwarz
