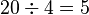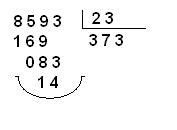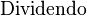División (matemática) para niños

En las matemáticas, la división es una operación que nos ayuda a saber cuántas veces un número (llamado divisor) cabe dentro de otro número (llamado dividendo). El resultado de esta operación se llama cociente. Piensa en la división como la operación contraria a la multiplicación. Por ejemplo, si sabes que 4 multiplicado por 5 es 20, entonces 20 dividido por 4 es 5.

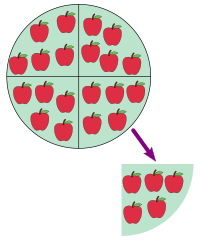
Hay dos tipos principales de división: la división "exacta", donde no sobra nada, y la división "con resto" o "residuo", donde sí sobra algo. Por ejemplo, si repartes 20 manzanas entre 4 personas, cada una recibe 5 manzanas y no sobra ninguna. Pero si repartes 21 manzanas entre 4 personas, cada una recibe 5 manzanas y sobra 1.

Para que la división siempre dé un número sin que sobre nada, usamos otros tipos de números, como los números racionales o los números reales. En estos casos, la división es la operación inversa de la multiplicación. Es decir, si a Plantilla:= c / b, significa que a × b Plantilla:= c, siempre y cuando b no sea cero. Dividir por cero no está permitido en matemáticas.

¿Qué es la división y cómo funciona?

La división se puede entender de dos maneras:

• Como reparto: Si tienes 20 manzanas y las quieres repartir en 5 grupos iguales, ¿cuántas manzanas habrá en cada grupo? La respuesta es 4. Esto se escribe como 20 / 5 = 4.
• Como agrupación: Si tienes 20 manzanas y quieres saber cuántos grupos de 5 manzanas puedes formar, ¿cuántos grupos harías? La respuesta es 4.

En el ejemplo 20 / 5 = 4:

• El dividendo es 20 (lo que se va a dividir).
• El divisor es 5 (el número por el que se divide).
• El cociente es 4 (el resultado de la división).

¿Qué pasa con el resto?

A veces, al dividir números, no obtenemos un resultado exacto. Por ejemplo, 10 / 3 no da un número entero. En este caso, 10 dividido por 3 es 3, y sobra 1. Ese "1" es el resto o residuo.

Cuando el resto se expresa como una fracción, el resultado es un número racional. Por ejemplo, 10 dividido por 3 es 3 1/3 o aproximadamente 3.33.... El conjunto de todos los números racionales se forma al incluir todos los resultados posibles de divisiones de números enteros.

Propiedades importantes de la división

La división tiene algunas propiedades que la hacen diferente de la suma o la multiplicación:

• No es conmutativa: Esto significa que el orden de los números importa. Por ejemplo, a / b no es lo mismo que b / a. (5 \div 3 \neq 3 \div 5).
• No es asociativa: Si tienes varias divisiones seguidas, el orden en que las haces puede cambiar el resultado. Por ejemplo, (24 / 6) / 2 Plantilla:= 2, pero 24 / (6 / 2) Plantilla:= 8.
• Es distributiva por la derecha: Puedes dividir una suma o resta por un número, y es lo mismo que dividir cada parte y luego sumar o restar los resultados. Por ejemplo, {{{1}}}.
• No es distributiva por la izquierda: No puedes dividir un número por una suma o resta de la misma manera. Por ejemplo, \frac{a}{b + c} \;\ne\; (a/b) + (a/c).

¿Cómo se escribe la división?

La división se puede escribir de varias maneras:

• Como fracción: Es la forma más común en matemáticas y ciencias. El dividendo va arriba y el divisor abajo. Por ejemplo, \tfrac{3}{4} se lee "tres dividido cuatro".
• Con una barra oblicua: 3/4. Esta es muy usada en computadoras.
• Con el símbolo de óbelo: \div . Este es el signo que ves en las calculadoras.
• Con dos puntos: : o ;.

Algoritmos para dividir

Un algoritmo es un conjunto de pasos para resolver un problema. Para la división, el método más conocido es la división larga. Este método nos permite dividir números grandes paso a paso.

Ejemplo de una división larga.

La división larga se representa con un diagrama especial:

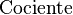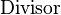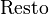También se puede usar una "tabla elemental" de división, similar a las tablas de multiplicar, donde ya están los resultados.

División de diferentes tipos de números

La división se aplica a distintos tipos de números, y el resultado puede variar:

División de números naturales

Los números naturales son los que usamos para contar (0, 1, 2, 3...). Si dividimos un número natural a entre otro número natural b (que no sea cero), obtenemos un cociente c si a es un múltiplo exacto de b. Si no es exacto, siempre podemos encontrar un cociente q y un resto r que cumplen la relación: {{{1}}}, donde el resto r es menor que el divisor b.

División de números enteros

Los números enteros incluyen los naturales, sus negativos y el cero (...-2, -1, 0, 1, 2...). Al dividir dos números enteros, el resultado no siempre es otro entero. Por ejemplo, 26 dividido por 11 no es un entero. En estos casos, podemos:

• Decir que no se puede dividir exactamente.
• Dar una respuesta aproximada con decimales (como 2.36).
• Dar la respuesta como una fracción (\tfrac{26}{11}).
• Dar la respuesta como un cociente y un resto (26 dividido por 11 es 2 con un resto de 4). Esta es la división euclídea.

Existen "criterios de divisibilidad" que son reglas rápidas para saber si un número entero se puede dividir exactamente por otro (por ejemplo, un número es divisible por 2 si termina en 0, 2, 4, 6 u 8).

División de números racionales

Los números racionales son aquellos que se pueden escribir como una fracción (como 1/2, 3/4, -5/7). La división de dos números racionales siempre es posible, siempre que el divisor no sea cero. Para dividir fracciones, se multiplica la primera fracción por la inversa de la segunda: {{math display="block">{p/q \over r/s} = {p \over q} \times {s \over r} = {ps \over qr}.</math}}

División de números reales

Los números reales incluyen todos los números racionales e irracionales (como pi o la raíz cuadrada de 2). El resultado de dividir dos números reales es otro número real, siempre que el divisor no sea cero. Se define como a/b = c si y solo si a = cb y b ≠ 0.

División de números complejos

Los números complejos son números que tienen una parte real y una parte imaginaria. El resultado de dividir dos números complejos es otro número complejo, siempre que el divisor no sea cero. Se calcula con una fórmula específica que combina las partes reales e imaginarias.

Conceptos relacionados con la división

• Algoritmo de la división: Los pasos para realizar una división.
• División larga: El método paso a paso para dividir números grandes.
• Divisibilidad: La propiedad de un número de poder ser dividido exactamente por otro.
• Razón (matemática): Una comparación entre dos cantidades usando la división.

Véase también

En inglés: Division (mathematics) Facts for Kids