Distribución normal multivariada para niños
En el mundo de la probabilidad y la estadística, la distribución normal multivariante es una herramienta muy útil. También se le conoce como distribución gaussiana multivariante. Imagina que la conocida distribución normal (la de la "campana de Gauss") describe una sola cosa, como la altura de las personas. Esta distribución multivariante es su versión "ampliada". Nos ayuda a entender cómo se comportan varias cosas a la vez. Por ejemplo, cómo se relacionan la altura y el peso de las personas.
Contenido
¿Qué es una Distribución Normal Multivariante?
Una distribución normal multivariante describe cómo se distribuyen varios datos juntos. Piensa en un grupo de características que están relacionadas. Por ejemplo, la altura, el peso y la edad de un grupo de estudiantes.
Entendiendo los Parámetros
Para describir esta distribución, necesitamos dos cosas principales:
- Un vector de medias (representado con la letra griega
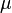): Es como el promedio de cada una de las características. Si tenemos altura y peso, este vector nos diría la altura promedio y el peso promedio. - Una matriz de covarianza (representada con la letra griega
): Esta matriz nos dice dos cosas importantes. Primero, cuánto varían los datos de cada característica por separado. Segundo, cómo se relacionan entre sí las diferentes características. Por ejemplo, si las personas más altas tienden a pesar más.
¿Cómo se ve?
Si la distribución normal simple es una campana, la multivariante es como una campana en varias dimensiones. En dos dimensiones, se vería como una colina o una montaña. Los puntos más altos de la "colina" son donde es más probable encontrar los datos.
| Tipo de distribución de probabilidad |
|---|
    |
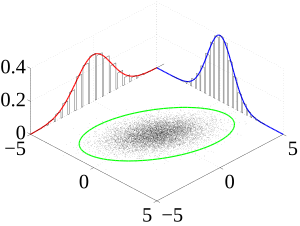
| Muchas observaciones de muestras (en negro) se observan a partir de una distribución de probabilidad conjunta. También se muestran las densidades marginales. |
La imagen de la derecha muestra cómo se verían muchos puntos de datos (en negro) que siguen una distribución normal multivariante. También puedes ver cómo se distribuyen individualmente las características X e Y.
¿Por qué es importante?
Esta distribución es fundamental en muchos campos. Se usa en ciencia, ingeniería y economía. Ayuda a crear modelos que predicen el comportamiento de sistemas complejos. Por ejemplo, en finanzas, para entender cómo se mueven juntos los precios de diferentes acciones.
Propiedades Clave
Las distribuciones normales multivariantes tienen características especiales que las hacen muy útiles.
Combinando Variables Normales
Una propiedad interesante es que si tienes varias variables que siguen una distribución normal multivariante, y las combinas de una manera sencilla (como sumarlas o multiplicarlas por un número), el resultado también seguirá una distribución normal. Esto simplifica mucho los cálculos.
¿Independencia y Correlación son lo mismo?
En estadística, a veces se confunden los términos "independiente" e "incorrelado".
- Incorrelado significa que no hay una relación lineal directa entre las variables. Es decir, si una aumenta, la otra no tiene por qué aumentar o disminuir de forma predecible.
- Independiente significa que el valor de una variable no afecta en absoluto el valor de la otra.
Para la distribución normal multivariante, hay una regla especial: si dos o más de sus componentes no están relacionadas linealmente (son incorreladas), entonces son también independientes. Esto no siempre es cierto para otras distribuciones.
Sin embargo, ten cuidado: si tienes dos variables que individualmente son normales y no están relacionadas linealmente, no significa que su combinación conjunta sea una distribución normal multivariante. Es un error común.
Transformando los Datos
Si tomas un conjunto de datos que sigue una distribución normal multivariante y le aplicas una transformación matemática simple (como sumarle un número o multiplicarlo por una matriz), los datos transformados seguirán siendo una distribución normal multivariante. Esto es muy útil para analizar datos.
Sumando Distribuciones Normales
Imagina que tienes varios grupos de datos, y cada grupo sigue una distribución normal multivariante. Si sumas estos grupos de datos (siempre que sean independientes entre sí), el resultado también será una distribución normal multivariante. La media del resultado será la suma de las medias, y la matriz de covarianza será la suma de las matrices de covarianza.
Cómo Usamos la Distribución Normal Multivariante
Esta herramienta matemática se aplica en muchos pasos del análisis de datos.
Encontrar los Parámetros
Cuando trabajamos con datos reales, no conocemos los valores exactos de la media y la matriz de covarianza. Usamos métodos especiales, como el de "máxima verosimilitud", para estimar estos valores a partir de los datos que tenemos. Es como intentar adivinar el centro de la "colina" y su forma, basándonos en los puntos que hemos medido.
Comprobando si los Datos Encajan
A veces, queremos saber si un conjunto de datos que hemos recogido realmente se ajusta a una distribución normal multivariante. Para esto, existen "tests de normalidad multivariante". Son pruebas estadísticas que nos ayudan a decidir si nuestros datos se parecen lo suficiente a esta distribución. Si el resultado de la prueba es muy bajo, significa que los datos probablemente no siguen este patrón.
Creando Datos Similares
También podemos usar esta distribución para "simular" o crear datos artificiales. Esto es útil para probar modelos o para entender cómo se comportarían los datos en diferentes situaciones. Para hacerlo, se usan cálculos matemáticos complejos que generan números aleatorios que siguen el patrón de la distribución normal multivariante.
Véase también
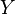
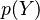
En inglés: 