Diagrama conmutativo para niños
Un diagrama conmutativo es un tipo especial de dibujo que se usa en matemática, especialmente en una rama llamada teoría de categorías. Imagina que es como un mapa donde tienes varios puntos (llamados objetos o vértices) y caminos que los conectan (llamados flechas o morfismos). La característica principal de un diagrama conmutativo es que, si empiezas en un punto y sigues diferentes caminos para llegar a otro punto, el resultado final siempre será el mismo. Es como si todas las rutas posibles entre dos lugares te llevaran al mismo destino.
Estos diagramas son muy importantes en la teoría de categorías, de la misma manera que las ecuaciones son importantes en el álgebra. Nos ayudan a visualizar y entender relaciones complejas entre diferentes elementos matemáticos. A veces, un diagrama puede no ser conmutativo, lo que significa que seguir diferentes caminos no lleva al mismo resultado. Para dejar claro que un diagrama sí cumple esta propiedad, se suelen usar frases como "este diagrama conmutativo" o "el diagrama conmuta".
Contenido
Historia de los Diagramas Conmutativos
La idea de los diagramas conmutativos está muy ligada al desarrollo de las matemáticas, sobre todo a la teoría de categorías. Estos diagramas son dibujos que muestran cómo se relacionan diferentes elementos matemáticos, como grupos de números o formas geométricas, y las funciones que los conectan. Aseguran que si combinas varias funciones de ciertas maneras, el resultado será el mismo. Esta forma de pensar surgió poco a poco, a medida que los matemáticos buscaban maneras de entender y representar ideas abstractas.
La idea de usar diagramas para mostrar relaciones matemáticas empezó a verse en el siglo XIX, cuando matemáticos como Évariste Galois y Augustin-Louis Cauchy empezaron a organizar las relaciones algebraicas de forma más clara. Sin embargo, el nombre "diagrama conmutativo" no se usó hasta mediados del siglo XX. Fue entonces cuando la teoría de categorías se convirtió en una parte formal de las matemáticas, gracias a trabajos de matemáticos como Samuel Eilenberg y Saunders Mac Lane. Ellos introdujeron los diagramas conmutativos como herramientas visuales para describir las propiedades de las funciones y las estructuras matemáticas de una forma más fácil de entender.
Los diagramas conmutativos nos permiten ver claramente cómo las combinaciones de funciones cumplen ciertas igualdades. Esto es fundamental en muchas áreas de las matemáticas, como el álgebra, la topología (el estudio de las formas) y la geometría. Con el tiempo, estos diagramas se han vuelto una herramienta central para los matemáticos, ayudando tanto a demostrar teoremas como a visualizar conceptos que son difíciles de imaginar.
Ejemplos de Diagramas Conmutativos
Los diagramas conmutativos se usan para representar muchas ideas matemáticas. Aquí te mostramos algunos ejemplos sencillos:
¿Cómo se ve un diagrama conmutativo?
Un diagrama conmutativo puede tener diferentes formas, pero siempre incluye puntos (objetos) y flechas (morfismos).
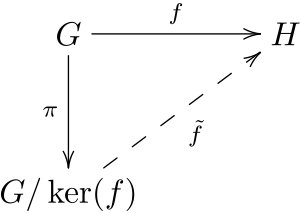
En el diagrama de arriba, que representa el primer teorema de isomorfía, la conmutatividad significa que si sigues el camino de la flecha `f`, obtendrás el mismo resultado que si sigues el camino de `π` y luego `f̃`.
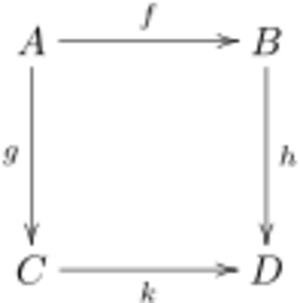
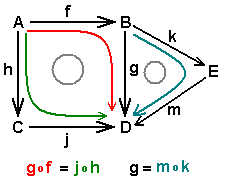
Este es un ejemplo de un cuadrado conmutativo. Aquí, la conmutatividad significa que si sigues el camino de `f` y luego `h`, el resultado es el mismo que si sigues el camino de `g` y luego `k`. Es decir, `h` compuesto con `f` es igual a `k` compuesto con `g`.
Símbolos en los Diagramas
En los textos de álgebra, las flechas en los diagramas pueden tener diferentes formas para indicar el tipo de relación que representan:
- Una flecha con un gancho (
 ) indica un monomorfismo, que es como una función "inyectiva" (cada elemento de inicio va a un elemento diferente al final).
) indica un monomorfismo, que es como una función "inyectiva" (cada elemento de inicio va a un elemento diferente al final). - Una flecha con doble punta (
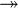 ) indica un epimorfismo, que es como una función "sobreyectiva" (todos los elementos del final son alcanzados por al menos un elemento del inicio).
) indica un epimorfismo, que es como una función "sobreyectiva" (todos los elementos del final son alcanzados por al menos un elemento del inicio). - Una flecha con una tilde encima (
 ) indica un isomorfismo, que es una función que tiene una inversa, como si fuera un "gemelo" del objeto original.
) indica un isomorfismo, que es una función que tiene una inversa, como si fuera un "gemelo" del objeto original. - Una flecha punteada o a trazos suele indicar que existe una función especial que hace que el diagrama sea conmutativo, si el resto de las condiciones se cumplen.
A veces, los libros no explican el significado de estas flechas, pero es útil conocerlas.
¿Cómo se verifica la conmutatividad?
Entender si un diagrama es conmutativo es bastante sencillo. Un diagrama es conmutativo si todos los pequeños polígonos (triángulos, cuadrados, etc.) que lo forman también son conmutativos. Es decir, si cada "circuito" dentro del diagrama cumple la regla de que todos los caminos entre dos puntos llevan al mismo resultado.
Persecución de Diagramas
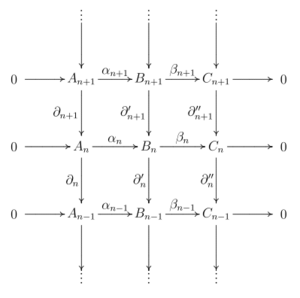
La persecución de diagramas (también llamada "cacería" o "búsqueda") es un método que usan los matemáticos para demostrar cosas, especialmente en un área llamada álgebra homológica. Imagina que tienes un diagrama conmutativo y quieres probar algo sobre él. Con este método, sigues los elementos a través de las flechas del diagrama, usando las propiedades de las funciones (como si son inyectivas o sobreyectivas).
Es como si "cazaras" o "atraparas" elementos moviéndote por el diagrama hasta que llegas al resultado que quieres demostrar. El diagrama en sí es una ayuda visual, pero la demostración es un argumento lógico que sería válido incluso sin el dibujo.
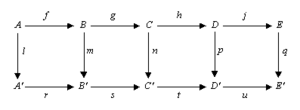
Algunos ejemplos famosos de demostraciones que usan la persecución de diagramas son las que se basan en el lema de los cinco, el lema de la serpiente, el lema zig-zag y el lema de los nueve.
Diagramas en Teorías de Categorías Más Avanzadas
En matemáticas, la teoría de categorías superiores es una parte más avanzada de la teoría de categorías. Aquí, algunas igualdades se reemplazan por flechas adicionales para estudiar con más detalle la estructura detrás de esas igualdades. Esto se usa mucho en topología algebraica, que estudia las propiedades de los espacios que no cambian cuando se estiran o doblan.
En estas teorías más avanzadas, no solo se consideran objetos y flechas, sino también "flechas entre flechas", "flechas entre flechas entre flechas", y así sucesivamente. Por ejemplo, la categoría de categorías pequeñas, llamada Cat, es una "categoría 2". Esto significa que tiene objetos (que son categorías), flechas (que son funciones entre categorías, llamadas "funtores") y también flechas entre esas flechas (llamadas "transformaciones naturales").
En este tipo de entornos, los diagramas conmutativos pueden incluir estas flechas de nivel superior, que a menudo se representan con una doble flecha (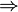 ).
).
Por ejemplo, el siguiente diagrama muestra dos categorías, C y D, con dos funtores F y G que van de C a D, y una transformación natural α que va de F a G:
En una categoría 2, hay diferentes formas de combinar las flechas (composición vertical y horizontal), y estas también se pueden representar con diagramas.
Diagramas como Funtores
Un diagrama conmutativo en una categoría C puede verse como un "functor" (una especie de función especial) que va de una categoría más pequeña (llamada categoría "indexada" o "J") a la categoría C. En la teoría de categorías, un diagrama es como una colección de objetos y funciones, organizados de una manera específica.
Para entenderlo mejor, piensa en una lista de conjuntos de números. Un diagrama es similar, pero en lugar de solo conjuntos, también incluye las relaciones (flechas) entre ellos.
De manera más formal, un diagrama conmutativo es una forma visual de representar un diagrama que está "indexado" por un conjunto parcialmente ordenado. Esto significa que:
- Se dibuja un punto (nodo) por cada objeto en la categoría indexada.
- Se dibuja una flecha por cada relación básica entre los objetos.
- Se omiten las flechas que representan la "identidad" (un objeto relacionado consigo mismo) y las flechas que se pueden formar combinando otras flechas.
- La conmutatividad del diagrama (que diferentes combinaciones de flechas entre dos objetos dan el mismo resultado) significa que solo hay una forma de ir de un objeto a otro en esa categoría.
Por otro lado, si tienes un diagrama conmutativo, puedes usarlo para definir una categoría especial:
- Los objetos de esta categoría son los puntos (nodos) del diagrama.
- Hay una flecha entre dos objetos si existe un camino directo entre ellos en el diagrama.
- La regla es que esta flecha es única (cualquier combinación de flechas que vaya del mismo punto de inicio al mismo punto final es la misma).
Es importante saber que no todos los diagramas son conmutativos. Un diagrama es una idea más general. Por ejemplo, un diagrama con un solo objeto y una flecha que va de ese objeto a sí mismo, o un diagrama con dos objetos y dos flechas paralelas entre ellos, no tienen por qué ser conmutativos. Además, a veces los diagramas pueden ser demasiado grandes o complejos para dibujarlos.
Véase también
 En inglés: Commutative diagram Facts for Kids
En inglés: Commutative diagram Facts for Kids
- Diagrama matemático
- Lema de los cinco
- Lema de la serpiente