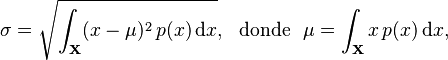Desviación típica para niños
En estadística, la desviación estándar (también conocida como desviación típica) es una medida que nos ayuda a entender qué tan dispersos o separados están los números en un grupo de datos. Se representa con la letra griega sigma minúscula (σ) o la letra latina s.
Si la desviación estándar es pequeña, significa que la mayoría de los números en el grupo están muy cerca del promedio (o valor central). Si la desviación estándar es grande, indica que los números están más extendidos y alejados del promedio.
|
La desviación estándar se calcula como la raíz cuadrada de la varianza. La varianza es el promedio de las diferencias al cuadrado entre cada número y el promedio del grupo.
Una ventaja importante de la desviación estándar es que se expresa en las mismas unidades que los datos originales. Por ejemplo, si mides alturas en centímetros, la desviación estándar también estará en centímetros.
Además de mostrar qué tan variables son los datos, la desviación estándar se usa para saber qué tan confiables son las conclusiones de un estudio. Por ejemplo, en las encuestas de opinión, el "margen de error" se basa en la desviación estándar. Esto nos dice cuánto podrían variar los resultados si la misma encuesta se hiciera muchas veces.
Es importante saber que la desviación estándar de un grupo completo de datos (una "población") es diferente de la desviación estándar de una pequeña parte de esos datos (una "muestra"). Sin embargo, están relacionadas.
Cuando los científicos analizan datos de experimentos, a menudo consideran que un resultado es importante si se aleja al menos dos desviaciones estándar del promedio. Esto les ayuda a distinguir entre cambios reales y variaciones normales o errores al medir.
Contenido
Desviación Estándar: ¿Qué es y para qué sirve?
La desviación estándar nos ayuda a entender la dispersión de los datos. Imagina que tienes un grupo de amigos y quieres saber qué tan parecidas son sus alturas. Si la desviación estándar es pequeña, significa que todos tienen alturas muy similares. Si es grande, significa que hay mucha diferencia entre la altura del más alto y el más bajo.
¿Cómo se calcula la Desviación Estándar?
Para calcular la desviación estándar, se siguen estos pasos:
- Primero, se calcula el promedio (la media) de todos los números.
- Luego, se resta el promedio a cada número del grupo.
- Esos resultados se elevan al cuadrado.
- Se suman todos esos resultados al cuadrado.
- Esa suma se divide por el número total de datos (o por el número de datos menos uno, si es una muestra).
- Finalmente, se calcula la raíz cuadrada de ese último resultado.
Ejemplos prácticos de Desviación Estándar
Aquí veremos algunos ejemplos para entender mejor cómo funciona la desviación estándar.
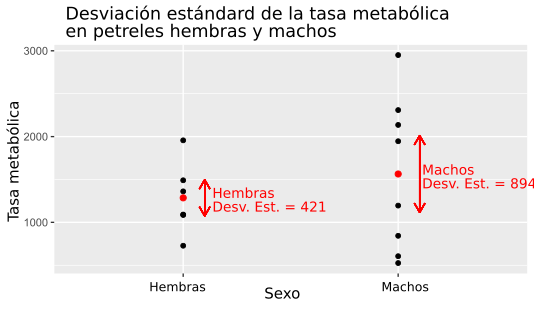
Ejemplo 1: Tasa metabólica de petreles
Un estudio midió la tasa metabólica (la energía que usan) de 8 petreles machos y 6 hembras. Los datos fueron:
| Sexo | Tasa metabólica | Sexo | Tasa metabólica |
|---|---|---|---|
| Macho | 525.8 | Hembra | 727.7 |
| Macho | 605.7 | Hembra | 1086.5 |
| Macho | 843.3 | Hembra | 1091.0 |
| Macho | 1195.5 | Hembra | 1361.3 |
| Macho | 1945.6 | Hembra | 1490.5 |
| Macho | 2135.6 | Hembra | 1956.1 |
| Macho | 2308.7 | ||
| Macho | 2950.0 |
A simple vista, parece que la tasa metabólica de los machos varía más que la de las hembras.
Para las hembras, el promedio de la tasa metabólica es 1285.5. La desviación estándar para las hembras se calcula así:
- Se resta el promedio a cada valor y se eleva al cuadrado. Por ejemplo, para la primera hembra: (727.7 - 1285.5)² = (-557.8)² = 311140.84.
- Se suman todos esos resultados al cuadrado: 886047.09.
- Se divide por el número de hembras menos 1 (6-1=5): 886047.09 / 5 = 177209.418.
- Se saca la raíz cuadrada: √177209.418 ≈ 420.69.
La desviación estándar para las hembras es aproximadamente 420.69. Para los machos, un cálculo similar da una desviación estándar de 894.37, que es casi el doble. Esto confirma que la tasa metabólica de los machos es más variable.
Ejemplo 2: Calificaciones de alumnos
Imagina que las calificaciones de 8 alumnos en una clase son: 2, 4, 4, 4, 5, 5, 7, 9. El promedio de estas calificaciones es 5. Para calcular la desviación estándar de esta población completa:
- Restamos el promedio (5) a cada calificación y elevamos el resultado al cuadrado:
* (2-5)² = 9 * (4-5)² = 1 * (4-5)² = 1 * (4-5)² = 1 * (5-5)² = 0 * (5-5)² = 0 * (7-5)² = 4 * (9-5)² = 16
- Sumamos estos resultados: 9 + 1 + 1 + 1 + 0 + 0 + 4 + 16 = 32.
- Dividimos la suma por el número total de alumnos (8): 32 / 8 = 4. Este es el valor de la varianza.
- La desviación estándar es la raíz cuadrada de la varianza: √4 = 2.
La desviación estándar de las calificaciones es 2. Esto nos dice que las calificaciones no están muy dispersas del promedio de 5.
Ejemplo 3: Edades de niños
Considera las edades de un grupo de 6 niños: {4, 1, 11, 13, 2, 7}. 1. Calcular el promedio: (4 + 1 + 11 + 13 + 2 + 7) / 6 = 38 / 6 ≈ 6.33. 2. Calcular la desviación estándar (para una muestra, dividimos por n-1): * (4 - 6.33)² = (-2.33)² = 5.43 * (1 - 6.33)² = (-5.33)² = 28.41 * (11 - 6.33)² = (4.67)² = 21.81 * (13 - 6.33)² = (6.67)² = 44.49 * (2 - 6.33)² = (-4.33)² = 18.75 * (7 - 6.33)² = (0.67)² = 0.45 * Suma de los cuadrados: 5.43 + 28.41 + 21.81 + 44.49 + 18.75 + 0.45 = 119.34 * Dividir por (6-1) = 5: 119.34 / 5 = 23.87 * Raíz cuadrada: √23.87 ≈ 4.88.
La desviación estándar de las edades es aproximadamente 4.88. Esto indica que las edades de los niños están bastante dispersas alrededor del promedio de 6.33 años.
Ejemplo 4: Estatura de hombres adultos
En Estados Unidos, la estatura promedio de los hombres adultos es de unos 177.8 cm, con una desviación estándar de aproximadamente 7.62 cm. Esto significa que la mayoría de los hombres (alrededor del 68%) tienen una altura entre 170.18 cm y 185.42 cm (177.8 ± 7.62 cm). Casi todos los hombres (alrededor del 95%) tienen una altura entre 162.56 cm y 193.04 cm (177.8 ± 2 veces 7.62 cm). Si la desviación estándar fuera cero, todos los hombres medirían exactamente 177.8 cm. Si fuera muy grande, como 50.8 cm, las alturas variarían mucho más.
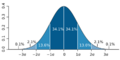
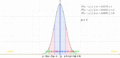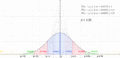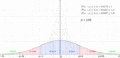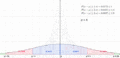
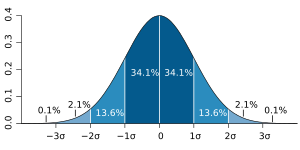
Desviación Estándar en la vida real: Regla 68-95-99.7
Cuando los datos siguen una distribución normal (una forma de campana), la desviación estándar nos da una idea muy clara de dónde se encuentran la mayoría de los datos.
- Aproximadamente el 68% de los datos están dentro de 1 desviación estándar del promedio.
- Aproximadamente el 95% de los datos están dentro de 2 desviaciones estándar del promedio.
- Aproximadamente el 99.7% de los datos están dentro de 3 desviaciones estándar del promedio.
Esta es la "regla empírica" o "regla 68-95-99.7". Es muy útil para entender rápidamente la distribución de un conjunto de datos.
| Intervalo de Confianza |
Proporción dentro | Proporción fuera | |
|---|---|---|---|
| Porcentaje | Porcentaje | Fracción | |
| 0.318 639 σ | 25 % | 75 % | 3 / 4 |
| 0,674490 σ | 50 % | 50 % | 1 / 2 |
| 0,994458 σ | 68 % | 32 % | 1 / 3,125 |
| 1 σ | 68,2689492 % | 31,7310508 % | 1 / 3,1514872 |
| 1,281552 σ | 80 % | 20 % | 1 / 5 |
| 1,644854 σ | 90 % | 10 % | 1 / 10 |
| 1,959964 σ | 95 % | 5 % | 1 / 20 |
| 2 σ | 95,4499736 % | 4,5500264 % | 1 / 21,977895 |
| 2,575829 σ | 99 % | 1 % | 1 / 100 |
| 3 σ | 99,7300204 % | 0,2699796 % | 1 / 370,398 |
| 3,290527 σ | 99,9 % | 0,1 % | 1 / 1000 |
| 3,890592 σ | 99,99 % | 0,01 % | 1 / 10 000 |
| 4 σ | 99,993666 % | 0,006334 % | 1 / 15 787 |
| 4,417173 σ | 99,999 % | 0,001 % | 1 / 100 000 |
| 4.5 σ | 99,9993204653751 % | 0,0006795346249 % | 3.4 / 1 000 000 (a cada lado de la media) |
| 4,891638 σ | 99,9999 % | 0,0001 % | 1 / 1 000 000 |
| 5 σ | 99,9999426697 % | 0,0000573303 % | 1 / 1 744 278 |
| 5,326724 σ | 99,99999 % | 0,00001 % | 1 / 10 000 000 |
| 5,730729 σ | 99,999999 % | 0,000001 % | 1 / 100 000 000 |
| 6 σ | 99,9999998027 % | 0,0000001973 % | 1 / 506 797 346 |
| 6,109410 σ | 99,9999999 % | 0,0000001 % | 1 / 1 000 000 000 |
| 6,466951 σ | 99,99999999 % | 0,00000001 % | 1 / 10 000 000 000 |
| 6,806502 σ | 99,999999999 % | 0,000000001 % | 1 / 100 000 000 000 |
| 7 σ | 99,9999999997440 % | 0,000000000256 % | 1 / 390 682 215 445 |
Breve historia de la Desviación Estándar
El término "desviación estándar" fue usado por primera vez por un matemático llamado Karl Pearson en 1894. Antes de él, otros matemáticos como Carl Friedrich Gauss usaban nombres como "error medio" para referirse a una idea similar.
Galería de imágenes
-
Una gráfica de la distribución normal (o curva en forma de campana, o curva de Gauss), donde cada banda tiene un ancho de una vez la desviación estándar (véase también: regla 68-95-99.7)
Véase también
 En inglés: Standard deviation Facts for Kids
En inglés: Standard deviation Facts for Kids


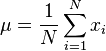 (Media aritmética)
(Media aritmética)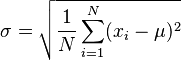 (Estimación sesgada del desvío estándar)
(Estimación sesgada del desvío estándar)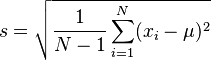 (Desvío estándar muestral (estimación insesgada))
(Desvío estándar muestral (estimación insesgada))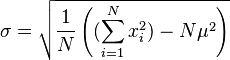 (Estimación sesgada del desvío estándar)
(Estimación sesgada del desvío estándar)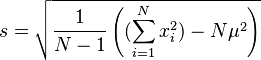 (Desvío estándar muestral (estimación insesgada))
(Desvío estándar muestral (estimación insesgada))