Curva de Bézier para niños
Las curvas de Bézier son una forma especial de dibujar líneas y formas suaves en computadoras. Se crearon alrededor de los años 1960 para ayudar a diseñar cosas como aviones y coches. Llevan el nombre de Pierre Bézier, un ingeniero que encontró una manera matemática de describir estas curvas. Gracias a él, se hicieron muy populares en los programas de diseño por computadora (CAD).
Contenido
¿Qué son las Curvas de Bézier?
Las curvas de Bézier son una herramienta fundamental en el diseño gráfico digital. Permiten crear líneas y formas muy precisas y suaves. Imagina que quieres dibujar una curva perfecta: con las curvas de Bézier, no solo defines el inicio y el final, sino también cómo se "dobla" la línea en el medio, usando puntos especiales que no están directamente sobre la curva.
¿Quién inventó las Curvas de Bézier?
Las curvas de Bézier fueron presentadas por primera vez en 1962 por el ingeniero francés Pierre Bézier. Él trabajaba en la empresa de automóviles Renault y las usó mucho para diseñar las diferentes partes de los coches. Sin embargo, las ideas detrás de estas curvas fueron desarrolladas por Paul de Casteljau, quien creó un algoritmo (una serie de pasos para resolver un problema) para calcularlas.
¿Cómo se usan en el diseño digital?
Cuando se inventó el lenguaje PostScript, que permite imprimir imágenes de alta calidad desde una computadora, se incluyó el método de Bézier para dibujar curvas. Por eso, muchos programas de diseño vectorial (que usan matemáticas para crear imágenes que no pierden calidad al agrandarse) como Adobe Illustrator, Corel Draw e Inkscape, tienen herramientas llamadas "pluma bézier" o "trazados bézier".
También se usan en programas de animación como Adobe Flash y en programas de edición de fotos como Photoshop y Gimp. Sirven para crear selecciones precisas, formas cerradas o trazos artísticos.
Puntos de anclaje y puntos de control
La idea principal es sencilla: un punto en una pantalla se define por sus coordenadas (como en un mapa). Para dibujar una línea recta entre dos puntos, solo necesitas sus posiciones. Pero para una curva, necesitas más. Los puntos donde la curva empieza o termina se llaman "puntos de anclaje" o "nodos". La forma de la curva se ajusta con unos puntos invisibles llamados "puntos de control" o "manejadores". Estos puntos "tiran" de la curva para darle la forma deseada.
Tipos de Curvas de Bézier
Existen diferentes tipos de curvas de Bézier, dependiendo de cuántos puntos de control se usen.
Curvas lineales de Bézier
La curva más simple es una línea recta. Si tienes dos puntos, P0 y P1, una curva lineal de Bézier es simplemente la línea que los une.
Curvas cuadráticas de Bézier
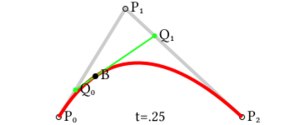
Para una curva cuadrática, necesitas tres puntos: P0, P1 y P2. La curva empieza en P0, se curva hacia P1 (que es un punto de control) y termina en P2. Las fuentes de letras TrueType (las que ves en tu computadora) usan este tipo de curvas.
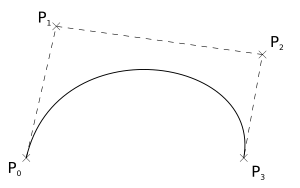
Curvas cúbicas de Bézier
Este es el tipo más común. Necesitas cuatro puntos: P0, P1, P2 y P3. La curva empieza en P0 y se dirige hacia P1. Luego, se curva y llega a P3, como si viniera de la dirección de P2. Normalmente, la curva no pasa por P1 ni por P2; estos puntos solo le dan dirección y forma. La distancia entre P0 y P1, por ejemplo, ayuda a determinar qué tan larga es la curva antes de cambiar de dirección.
Los sistemas modernos de gráficos, como PostScript y SVG, usan curvas cúbicas de Bézier para dibujar las formas.
¿Cómo se construyen las Curvas de Bézier?
La construcción de estas curvas se basa en un proceso de interpolación, es decir, de encontrar puntos intermedios.
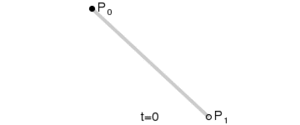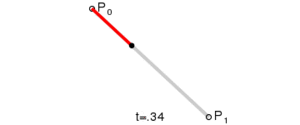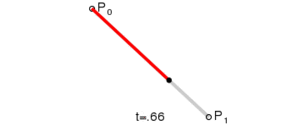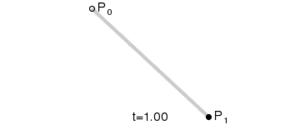
Curvas lineales
| Imagina que tienes un punto que se mueve desde P0 hasta P1. A medida que este punto se mueve, va dibujando la línea recta. |
Curvas cuadráticas
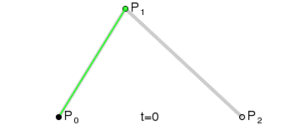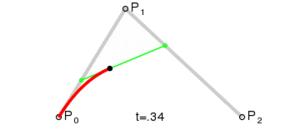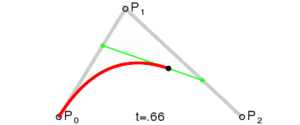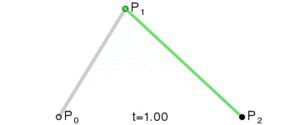
Para una curva cuadrática, se construyen puntos intermedios. Piensa en dos puntos que se mueven:
|
|
Curvas de órdenes superiores
Para curvas más complejas, se necesitan más puntos intermedios y más pasos. Por ejemplo, para una curva cúbica, se usan puntos que describen curvas lineales y luego puntos que describen curvas cuadráticas, hasta llegar a la curva final.
Usos de las Curvas de Bézier
Gráficos por computadora
Las curvas de Bézier son muy importantes en los gráficos por computadora para crear formas suaves. Como la curva siempre está dentro de un área definida por sus puntos de control (llamada "envolvente convexa"), es muy fácil manipularla. Puedes mover o rotar la curva simplemente moviendo sus puntos de control.
Las curvas cuadráticas y cúbicas son las más usadas. Las curvas más complejas son más difíciles de calcular. Para que las curvas se vean suaves cuando se unen varias, los puntos de control en la unión deben estar alineados.
Sonido y animación
Las curvas de Bézier también se usan para crear sonidos, en un proceso llamado síntesis de Bézier. Además, son muy útiles para describir cómo se mueven los objetos en las animaciones. Por ejemplo, puedes definir la trayectoria de un personaje o un objeto usando una curva de Bézier, lo que permite movimientos muy fluidos y naturales.
Galería de imágenes
Véase también
 En inglés: Bézier curve Facts for Kids
En inglés: Bézier curve Facts for Kids