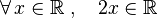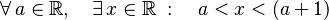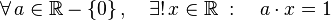robot de la enciclopedia para niños

Cuantificador para niños

Enciclopedia para niños
Para la categoría gramatical, véase Cuantificador (lingüística).

En la lógica formal, un cuantificador es una palabra o símbolo que nos ayuda a decir cuántas veces una característica o "propiedad" se cumple dentro de un grupo de cosas. Por ejemplo, nos permite decir si algo se cumple para todos los elementos de un grupo, o si se cumple para algunos de ellos.

Existen varios tipos de cuantificadores, los más usados son:

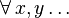 :\forall \, x, y \ldots  :Significa "Para todo x, y..." o "Todos los x, y...".

  • Cuantificador existencial

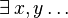 :\exists \, x, y \ldots  :Significa "Existe al menos un x, y..." o "Hay algún x, y...".

  • Cuantificador existencial único

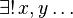 :\exists ! \, x, y \ldots  :Significa "Existe exactamente un x, y..." o "Hay solo un x, y...".

  • Negación del cuantificador existencial

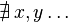 :\nexists \, x, y \ldots  :Significa "No existe ningún x, y..." o "No hay ningún x, y...".

Historia de los cuantificadores

¿Quién inventó los cuantificadores?

Un matemático, lógico y filósofo alemán llamado Gottlob Frege publicó un libro muy importante en 1879, llamado Begriffsschrift. En este libro, Frege sentó las bases de la lógica matemática moderna. Él fue el primero en desarrollar una forma clara y organizada de usar los cuantificadores.

¿Qué aportó Frege?

Frege introdujo nuevos símbolos, como 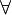\forall (para "para todo") y 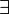\exist (para "existe"), que nos permiten hablar de cantidades de una manera más precisa en la lógica. Su trabajo fue fundamental para entender cómo funcionan las afirmaciones sobre grupos de cosas.

Su libro se dividió en varias partes:

  • La primera parte explicaba las ideas básicas y los símbolos, incluyendo los cuantificadores universales, la negación lógica (decir "no") y la condicional (decir "si... entonces...").
  • La segunda parte presentaba los axiomas, que son verdades que se aceptan sin necesidad de demostración.

¿Cómo se usan los cuantificadores en las afirmaciones?

Las afirmaciones que usan cuantificadores se escriben de una forma especial. Aquí te mostramos algunos ejemplos para entenderlo mejor:

  • \forall \, x \in \mathbb{R} \; , \quad 2x \in \mathbb{R}

 :Esto se lee: "Para todo número x que sea un número real (que pertenece a R), se cumple que el doble de x (2x) también es un número real".

  • \forall \, a \in \mathbb{R} , \quad \exists \, x \in \mathbb{R} \; : \quad a < x < (a + 1)

 :Esto se lee: "Para todo número a que sea un número real, existe un número x que también es real, de tal forma que x está entre a y a+1".

  • \forall \, a \in \mathbb{R}-\left\{{0}\right\} , \quad \exists ! \, x \in \mathbb{R} \; : \quad a \cdot x=1

 :Esto se lee: "Para todo número a que sea un número real y que no sea cero, existe un único número x que es real, de tal forma que a multiplicado por x es igual a 1".

Tipos de cuantificación

Cuantificación universal: "Para todos"

El cuantificador universal (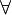\forall) se usa para decir que todos los elementos de un grupo cumplen con una característica específica. Por ejemplo:

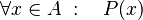
\forall x \in A \; : \quad P(x)
Se lee: "Para todo x que pertenece al grupo A, se cumple la característica P(x)".

Esto es como decir que el grupo A está formado por todos los elementos x de un grupo más grande (llamado U) que tienen la característica P(x).

Cuantificación existencial: "Existe al menos uno"

El cuantificador existencial (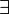\exists) se usa para indicar que hay uno o más elementos en un grupo que cumplen con una característica. No significa que sea el único, solo que hay al menos uno. Se escribe así:

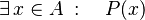
\exists \, x \in A \; : \quad P(x)
Se lee: "Existe al menos un x en el grupo A que cumple la característica P(x)".

Esto significa que el grupo de elementos x de A que cumplen P(x) no está vacío.

Cuantificación existencial única: "Existe solo uno"

El cuantificador existencial con marca de unicidad (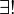\exists !) se usa para decir que hay un único elemento en un grupo que cumple una característica específica. Se escribe:

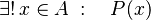
\exists ! \, x \in A \; : \quad P(x)

Se lee: "Existe un único elemento x del grupo A que cumple la característica P(x)".

Relaciones importantes entre cuantificadores

Los cuantificadores tienen relaciones entre sí que nos permiten cambiar la forma de una afirmación sin que cambie su significado.

  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \forall x \in A \ P(x) \qquad \longleftrightarrow \qquad \neg \exists x \in A\ \neg P(x)

 :Esto significa: "Para todo x de A, se cumple P(x) si y solo si no existe ningún x en A que no cumpla P(x)". Es decir, si todos cumplen algo, entonces no hay ninguno que no lo cumpla.

  • Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \exists x \in A\ P(x) \qquad \longleftrightarrow \qquad \neg \forall x\in A \ \neg P(x)

 :Esto significa: "Existe al menos un x en A que cumple P(x) si y solo si no es cierto que para todo x de A, no se cumpla P(x)". Es decir, si existe alguno que lo cumple, entonces no es verdad que ninguno lo cumpla.

Leyes de De Morgan para cuantificadores

Las leyes de De Morgan nos ayudan a entender cómo la negación afecta a los cuantificadores:

  • \neg \forall x P(x)\equiv \exists x \neg P(x)

 :Si no es cierto que "para todo x, P(x) es verdadero", entonces es lo mismo que decir que "existe al menos un x para el que P(x) es falso".

  • \neg \exists x P(x)\equiv \forall x \neg P(x)

 :Si no es cierto que "existe al menos un x para el que P(x) es verdadero", entonces es lo mismo que decir que "para todo x, P(x) es falso".

Orden de los cuantificadores

¿Importa el orden?

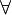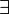El orden en que se usan los cuantificadores \forall y \exist es muy importante. Tienen una prioridad mayor que otros símbolos lógicos.

Por ejemplo, cuando escribimos 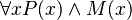\forall x P(x) \land M(x), la prioridad nos dice que primero debemos aplicar el cuantificador a 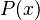P(x), es decir, se lee como 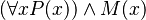(\forall x P(x)) \land M(x). Esto significa "Para todo x, P(x) es cierto, Y además, M(x) es cierto".

Si queremos que el cuantificador afecte a toda la expresión, debemos usar paréntesis. Por ejemplo, 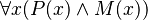\forall x (P(x) \land M(x)) significa "Para todo x, tanto P(x) como M(x) son ciertos".

Es un error común pensar que 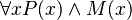\forall x P(x) \land M(x) es lo mismo que 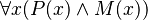\forall x (P(x) \land M(x)). No lo son, porque el orden de prioridad cambia el significado.

Véase también

Kids robot.svg En inglés: Quantifier (logic) Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Cuantificador&oldid=4891040»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Cuantificador para Niños. Enciclopedia Kiddle.