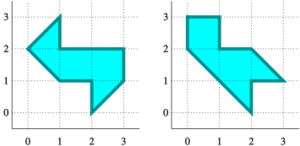Carolyn S. Gordon para niños
Datos para niños Carolyn S. Gordon |
||
|---|---|---|
 |
||
| Información personal | ||
| Nacimiento | 26 de diciembre de 1950 Charleston (Estados Unidos) |
|
| Nacionalidad | Estadounidense | |
| Educación | ||
| Educada en | ||
| Tesis doctoral | Grupos de isometría reductiva de variedades riemannianas homogéneas (1979) | |
| Supervisor doctoral | Edward Wilson | |
| Información profesional | ||
| Ocupación | Matemática | |
| Área | Geometría diferencial | |
| Cargos ocupados | President of the Association for Women in Mathematics (2003-2005) | |
| Empleador | Dartmouth College | |
| Miembro de |
|
|
| Distinciones |
|
|
Carolyn S. Gordon (nacida en 1950) es una destacada matemática y profesora. Actualmente, enseña matemáticas en el Dartmouth College. Es muy reconocida por su trabajo junto a David Webb y Scott A. Wolpert. Ellos respondieron a una pregunta famosa en matemáticas: "¿Puedes oír la forma de un tambor?".
Gordon ha recibido importantes reconocimientos por su trabajo. Ganó el Premio Chauvenet en 2001. También fue seleccionada para dar la Conferencia Noether en 2010.
Contenido
Primeros años y formación académica
Carolyn Gordon obtuvo su título de licenciatura en la Universidad Purdue. Después, continuó sus estudios avanzados en la Universidad Washington en San Luis. Allí, completó su doctorado en matemáticas en 1979.
Su director de tesis fue Edward Nathan Wilson. Su investigación doctoral se centró en los grupos de isometría de variedades homogéneas. Tras su doctorado, realizó una estancia de investigación en el Technion Israel Institute of Technology. También trabajó en la Universidad de Lehigh y en la Universidad de Washington.
Carrera profesional y descubrimientos
La profesora Gordon es famosa por su trabajo en geometría isoespectral. Esta área de las matemáticas se pregunta si el sonido de un objeto puede revelar su forma. Imagina un tambor: ¿su sonido nos diría cómo es su forma?
En 1966, el matemático Mark Kac planteó esta pregunta. Quería saber si la forma de un tambor se podía determinar por el sonido que produce. Otros matemáticos habían encontrado ejemplos complejos. Sin embargo, la pregunta para formas más simples, como las de dos dimensiones, seguía sin respuesta.
En 1992, Carolyn Gordon, junto con David Webb y Scott A. Wolpert, encontró la respuesta. Demostraron que dos formas diferentes pueden sonar exactamente igual. Crearon un par de regiones en un plano que tienen formas distintas pero producen los mismos sonidos. Puedes ver un ejemplo en la imagen de la derecha.
En investigaciones posteriores, Gordon y Webb crearon más ejemplos. Encontraron formas isoespectrales en el plano hiperbólico y en el espacio euclidiano.
Investigaciones adicionales
Gordon ha escrito más de 30 artículos sobre geometría isoespectral. Su trabajo incluye el estudio de variedades riemannianas cerradas que suenan igual. Estas variedades tienen la misma geometría local, pero su forma general es diferente. Se pueden encontrar usando un método llamado "método Sunada".
En 1993, descubrió variedades riemannianas isoespectrales que no son iguales en todas sus partes. Desde entonces, ha seguido trabajando con otros matemáticos para encontrar más ejemplos de este tipo.
También ha investigado cómo la clase de homología y el espectro de longitud se relacionan con las variedades isoespectrales. El espectro de longitud es la colección de todas las longitudes de los caminos cerrados en una forma.
Reconocimientos y premios
En 2001, Carolyn Gordon y David Webb recibieron el Premio Chauvenet. Este premio lo otorga la Mathematical Association of America. Lo ganaron por su artículo de 1996, "You can't hear the shape of a drum", publicado en la revista American Scientist.
En 1990, la American Mathematical Society le otorgó una beca especial. Fue por su destacada investigación al inicio de su carrera. En 1999, dio un importante discurso conjunto para la AMS y la MAA. En 2010, fue elegida para dar la prestigiosa Conferencia Noether.
En 2012, se convirtió en miembro de la American Mathematical Society y de la Asociación Estadounidense para el Avance de la Ciencia. En 2017, fue seleccionada como becaria de la Asociación de Mujeres en Matemáticas. Su trabajo fue destacado en la edición de marzo de 2018 de AMS Notices, como parte del Mes de la Historia de la Mujer.
Artículos destacados
Aquí tienes algunos de los trabajos más importantes de Carolyn Gordon:
- Gordon, Carolyn (2001), «Isospectral Deformations of Metrics on Spheres», Inventiones Mathematicae 145 (2): 317-331, Bibcode:2001InMat.145..317G, doi:10.1007/s002220100150.
- Gordon, Carolyn; Webb, David (1996), «You can't hear the shape of a drum», American Scientist 84 (January–February): 46-55, Bibcode:1996AmSci..84...46G.
- Gordon, Carolyn (1994), Isospectral Closed Riemannian Manifolds which are not Locally Isometric II, Contemporary Mathematics 173, American Mathematical Society, pp. 121-131, ISBN 9780821851852, doi:10.1090/conm/173/01821.
- Gordon, Carolyn; Webb, David; Wolpert, Scott (1992), «Isospectral plane domains and surfaces via Riemannian orbifolds», Inventiones Mathematicae 110: 1-22, Bibcode:1992InMat.110....1G, doi:10.1007/BF01231320.
- Gordon, Carolyn; Webb, David L.; Wolpert, Scott (1992), «One Cannot Hear the Shape of a Drum», Bulletin of the American Mathematical Society 27: 134-138, doi:10.1090/S0273-0979-1992-00289-6.
- Gordon, Carolyn; Wilson, Edward (1984), «Isospectral deformations of compact solvmanifolds», Journal of Differential Geometry 19: 241-256, doi:10.4310/jdg/1214438431.
Vida personal
Carolyn Gordon está casada con David Webb. Ella ha mencionado que criar a su hija, Annalisa, es una de las cosas que más alegría le ha dado en la vida.
Véase también
 En inglés: Carolyn S. Gordon Facts for Kids
En inglés: Carolyn S. Gordon Facts for Kids