robot de la enciclopedia para niños

Circunferencia goniométrica para niños

Enciclopedia para niños

La circunferencia goniométrica, también conocida como circunferencia unitaria o circunferencia trigonométrica, es un círculo muy especial en matemáticas. Su característica principal es que tiene un radio de una unidad de longitud. Generalmente, su centro se encuentra en el punto (0, 0) de un sistema de coordenadas en un plano.

Esta circunferencia es una herramienta muy útil para entender y trabajar con las razones trigonométricas y las funciones trigonométricas. Nos ayuda a visualizar cómo se relacionan los ángulos con los lados de los triángulos rectángulos.

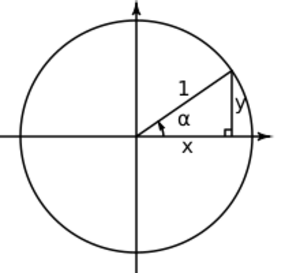
Si tomamos un punto (x, y) en la circunferencia unitaria, especialmente en el primer cuadrante (donde x e y son positivos), podemos formar un triángulo rectángulo. En este triángulo, 'x' e 'y' serían las longitudes de los catetos, y el hipotenusa tendría una longitud de 1 (porque es el radio de la circunferencia).

Aplicando el teorema de Pitágoras, que dice que en un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, obtenemos la siguiente ecuación:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + y^2 = 1^2 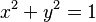x^2 + y^2 = 1

Esto significa que cualquier punto (x, y) que esté sobre la circunferencia unitaria debe cumplir esta ecuación.

¿Cómo se usan las funciones trigonométricas en la circunferencia unitaria?

Archivo:Circunferencia unidad y coordenadas
La circunferencia unitaria y el triángulo rectángulo que se forma.
Archivo:Circunferencia unidad y relación pitagórica
La relación de Pitágoras en la circunferencia unitaria.
Archivo:Circunferencia unidad y triángulo rectángulo
Un triángulo rectángulo dentro de la circunferencia unitaria.

Cuando tenemos un punto (x, y) en la circunferencia unitaria, y trazamos una línea desde el centro (0,0) hasta ese punto, esta línea forma un ángulo con el eje horizontal (eje X). A este ángulo lo llamamos 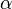\alpha \, .

Las principales funciones trigonométricas (seno, coseno y tangente) se pueden entender fácilmente usando este triángulo rectángulo auxiliar:

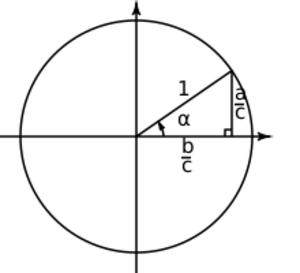
  • El seno de un ángulo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen(\alpha) ) es la relación entre el cateto opuesto al ángulo y la hipotenusa.

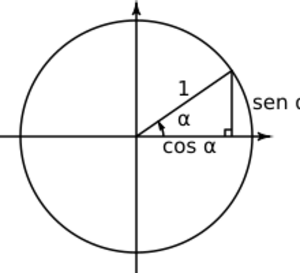
* En la circunferencia unitaria, el cateto opuesto es la coordenada 'y' del punto (x, y). * Como la hipotenusa es el radio y mide 1, el seno del ángulo es simplemente la coordenada 'y'. * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen(\alpha)= \frac{\text{cateto opuesto}}{\text{hipotenusa}} = \frac{y}{1} = y \,

  • El coseno de un ángulo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos(\alpha) ) es la relación entre el cateto adyacente (el que está junto al ángulo) y la hipotenusa.

* En la circunferencia unitaria, el cateto adyacente es la coordenada 'x' del punto (x, y). * Como la hipotenusa mide 1, el coseno del ángulo es simplemente la coordenada 'x'. * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos(\alpha)= \frac{\text{cateto adyacente}}{\text{hipotenusa}} = \frac{x}{1} = x \,

  • La tangente de un ángulo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tan(\alpha) ) es la relación entre el cateto opuesto y el cateto adyacente.

* En la circunferencia unitaria, esto es la coordenada 'y' dividida por la coordenada 'x'. * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tan(\alpha)= \frac{\text{cateto opuesto}}{\text{cateto adyacente}} = \frac{y}{x} \,

Funciones trigonométricas recíprocas

Además de seno, coseno y tangente, existen otras tres funciones trigonométricas que son sus "recíprocas" (es decir, 1 dividido por la función original):

  • La cosecante (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \csc (\alpha) ) es la recíproca del seno:

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \csc (\alpha) = \frac{1}{\sen (\alpha)}

  • La secante (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sec (\alpha) ) es la recíproca del coseno:

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sec (\alpha) = \frac{1}{\cos (\alpha)}

  • La cotangente (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cot (\alpha) ) es la recíproca de la tangente:

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cot (\alpha) = \frac{1}{\tan (\alpha)}

Estas funciones también se pueden visualizar y entender usando la circunferencia unitaria y la semejanza de triángulos.

Galería de imágenes

  • Unit-circle sin cos tan cot exsec excsc versin vercos coversin covercos

    Principales valores de las razones trigonométricas representados como segmentos en la circunferencia unitaria.

  • Unit circle angles

    Valores de los ángulos más comunes y sus coordenadas correspondientes en la circunferencia unitaria.

Véase también

Kids robot.svg En inglés: Unit circle Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Circunferencia_goniométrica&oldid=4840425»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Circunferencia goniométrica para Niños. Enciclopedia Kiddle.