Origami para niños
El origami (del japonés 折り紙) es un arte que consiste en doblar papel para crear figuras de muchas formas diferentes. Algunas de estas figuras son tan bonitas que parecen pequeñas esculturas de papel.
En el origami moderno, especialmente en estilos como el "puro" y el "pureland", no se usan tijeras ni pegamento. Sin embargo, algunos diseños tradicionales japoneses sí los utilizaban. Por eso, es importante saber que el origami es una parte de un arte más grande llamado papiroflexia, que incluye todas las técnicas de doblar papel, incluso si usan cortes o pegamento.
Lo especial del origami es que transforma una simple hoja de papel, que suele ser cuadrada o rectangular, en figuras de diferentes tamaños. Estas figuras pueden ser muy sencillas o increíblemente complejas. Con el origami se pueden representar muchas cosas de nuestro mundo: animales, plantas, objetos de la vida diaria, y hasta criaturas imaginarias.
El origami ha crecido mucho desde los años 60. Gracias a internet y a las asociaciones de origami en todo el mundo, se han descubierto y compartido nuevas técnicas. También se ha empezado a estudiar más la relación entre el origami y las matemáticas, algo que ha tomado mucha fuerza en los últimos 30 años. Con la llegada de las computadoras en los años 90, se ha podido mejorar cómo se usa el papel y crear nuevas bases para figuras muy complejas, como los insectos.
Contenido
Origen del término
La palabra "origami" viene de dos palabras japonesas: "ORI" (que significa doblar o plegar) y "KAMI" (que significa papel). Cuando se juntan, "kami" cambia a "gami", formando "origami".
En algunos países de habla hispana, como España, a este arte se le llama papiroflexia o cocotología. Sin embargo, en otros países hispanohablantes, se usa más la palabra "origami" para referirse al arte japonés de doblar papel, y "papiroflexia" para el arte de doblar papel en general.
Historia del Origami
El arte del origami, tal como lo conocemos hoy, es relativamente moderno y ha tenido grandes avances en los últimos años. Estamos viviendo una "edad de oro" del origami, donde la mayoría de los plegadores importantes están vivos y se han logrado muchos progresos en poco tiempo.
Momentos Clave en la Historia del Origami
- Alrededor del año 100 d.C.: China inventa el papel.
- Alrededor del año 600 d.C.: El papel llega a Japón.
- 1797: Se publica el primer libro de origami, llamado Hiden Senbazuru Orikata.
- 1845: Se publica el libro de figuras Kan no mado.
- 1935: Akira Yoshizawa inventa un sistema de símbolos para explicar los dobleces.
- 1960: Se crea el modelo del tren, que impulsa nuevas técnicas como el "box pleating".
- 1990: Meguro y Lang desarrollan la teoría del "empaquetamiento de círculos".
- 2011: Lang avanza en el "empaquetamiento de polígonos".
¿Cómo Nació el Origami?
El arte de doblar papel comenzó en China, probablemente en el siglo I o II. Llegó a Japón en el siglo VI y se volvió parte de sus tradiciones.
Durante el periodo Heian (del 794 al 1185), el origami era importante en las ceremonias de la nobleza. Doblar papel era un lujo que solo las personas ricas podían permitirse. Entre 1338 y 1573, en el periodo Muromachi, el papel se hizo más barato y el estilo de origami de una persona podía mostrar a qué grupo social pertenecía.
Entre 1603 y 1867, en el periodo Tokugawa, el arte se hizo popular para todos. En 1797, se documentaron las bases del pájaro y la rana en el libro Senbazuru Orikata.
El Origami en Occidente
El origami llegó a Occidente a través de los comerciantes que viajaban por la Ruta de la Seda. Es posible que apareciera cuando Marco Polo trajo el papel en el siglo XIII, aunque al principio los europeos preferían el pergamino.
El papel duraba menos que el pergamino, pero finalmente fue aceptado por ser más fácil de usar y más barato. La invención de la imprenta también ayudó a que se popularizara.
Sus orígenes en Occidente también se relacionan con la llegada de prisioneros chinos a Samarcanda en el año 751, quienes enseñaron a hacer y doblar papel. Como la religión musulmana no permitía representar figuras humanas o animales en el arte, se enfocaron en formas geométricas y en el estudio matemático de los patrones que se forman al doblar el papel. Estos patrones se usaron incluso en el diseño de edificios.
Hoy en día, existen muchos principios y teoremas relacionados con el doblado de papel, que han llevado a nuevos conceptos en matemáticas aplicadas. Después de que los árabes salieran de España, los españoles mantuvieron estos diseños y desarrollos, añadiendo formas inspiradas en la naturaleza.
El Encuentro entre Oriente y Occidente
Hace unos 150 años, Japón abrió sus puertas al mundo después de siglos de aislamiento. Esto tuvo un gran impacto en el origami. El primer libro de origami moderno, Hiden Senbazuru Orikata, marcó el inicio de esta nueva etapa.
En el origami clásico se podían recortar, pegar y pintar las figuras. Pero para el origami moderno, los maestros japoneses establecieron nuevas reglas: no usar tijeras, evitar la pintura y no usar pegamento. La figura debía lograrse solo doblando el papel, mostrando la belleza del material en su forma y color.
En la Exposición Universal de París en 1878, los conocimientos de origami de Oriente y Occidente se unieron, creando un solo arte. A finales del siglo XIX, Friedrich Fröbel incluyó el origami en sus métodos de enseñanza escolar. Fue adoptado rápidamente en los jardines de infancia japoneses porque ayudaba a enseñar figuras geométricas y ofrecía otros beneficios educativos. En esa época, un vendedor europeo llevó papel de colores a Tokio, lo que mejoró mucho la calidad de los modelos de origami.
El Origami en el Mundo Hispano
En los países de habla hispana, el escritor español Miguel de Unamuno fue quien realmente impulsó el origami alrededor de 1930. Antes de él, el origami no era muy conocido en España, ya que en la Europa medieval se usaba más el pergamino, que era un material más grueso que el papel de arroz oriental. Unamuno fue el primero en tomarse en serio el arte de hacer "pajaritas de papel".
Unamuno también escribió sobre la "cocotología", un término que él mismo creó para referirse al arte de doblar papel. Publicó varios libros sobre plegado, incluyendo un ensayo donde hablaba del origami.
Miguel de Unamuno tuvo una gran influencia en América del Sur, donde también se le considera el "padre de la papiroflexia hispanoamericana". Gracias a él, este arte ganó muchos seguidores y surgieron grandes artistas del papel, como el español Vicente Solórzano Sagredo y la argentina Ligia Montoya.
La Popularización del Arte
En la misma década de 1930, algunos educadores no valoraban el origami porque pensaban que no fomentaba la originalidad. Sin embargo, gracias a su larga historia, el origami recuperó su popularidad. Esto fue en gran parte por Akira Yoshizawa, un genio del origami del siglo XX que creó más de 50,000 trabajos. Él desarrolló nuevas formas de hacer figuras, poniendo énfasis en la belleza de la forma y la precisión.
A mediados del periodo Showa, Yoshizawa y Sam Randlett crearon un código internacional de símbolos para representar los dobleces de las figuras. Este sistema se usa hoy en día para enseñar a hacer origami. Gracias a este sistema, la publicación de libros de origami aumentó mucho, primero en Japón y luego en otros países. Esto llevó a la formación de grupos y asociaciones de origami en todo el mundo, como FOCA (ahora Origami USA) en 1958 y la Sociedad Británica de Papiroflexia en 1967.
El Pasado Reciente del Origami
Akira Yoshizawa es visto como el iniciador de una nueva era del origami. Inventó una simbología que aún se usa y revolucionó el arte con figuras nuevas y la técnica del plegado en húmedo. Él introdujo modelos en tres dimensiones, dando un gran impulso al arte de doblar papel.
Otro momento importante fue en 1960, con la aparición del tren de Emmanuel Mooser. Este modelo:
- Permitió diseñar objetos creados por el ser humano.
- Llevó al descubrimiento de la técnica "box pleating".
- Hizo posible diseñar figuras con muchas partes a partir de una sola hoja de papel.
- Fomentó el diseño de figuras en 3 dimensiones.
A principios de los años 90, surgió la teoría del "empaquetamiento de círculos" o "teoría del árbol", desarrollada por Toshiyuki Meguro y Robert J. Lang. Este método fue otro gran avance que abrió nuevas posibilidades para diseñar figuras.
La incorporación de las matemáticas, la optimización del papel y el uso de computadoras en diseños complejos han caracterizado los últimos años y han sentado las bases para las figuras complejas de hoy.
El Origami en la Actualidad
Hoy en día, el origami sigue avanzando gracias a la incorporación de las matemáticas y la computación. Se han descubierto teoremas y axiomas del origami que ayudan a entender su geometría. Programas de computadora, como los desarrollados por Robert Lang, optimizan el uso del papel para crear diseños complejos.
Los avances en la complejidad de las figuras han hecho necesario un papel más especializado. Michael LaFosse ha contribuido a crear el papel "Origamido", considerado uno de los mejores. Además, internet ha facilitado la comunicación entre los aficionados y las asociaciones de origami de diferentes países.
Muchos expertos creen que estamos en la "edad de oro" del origami, con muchos avances en pocos años y una gran variedad de artistas que comparten sus conocimientos a través de libros e internet. Algunos artistas destacados de los últimos 50 años incluyen a Kunihiko Kasahara, Eric Joisel, Tomoko Fuse, Robert Lang, John Montroll, Vicente Palacios y Peter Budai.
Tipos de Origami
Origami de Acción
El origami no solo crea figuras que se quedan quietas. También existen modelos que pueden moverse de formas ingeniosas. El origami de acción incluye figuras que vuelan, que necesitan ser infladas para completarse, o que mueven una parte al presionar o tirar de ellas. Un ejemplo famoso es el pájaro que aletea, un diseño tradicional japonés.
Origami Modular (Kusudama)
El origami modular consiste en unir varias piezas idénticas para formar un modelo completo. Las piezas suelen ser sencillas, pero el resultado final puede ser muy complejo. Muchos modelos modulares son bolas decorativas, como el kusudama. La diferencia es que el kusudama a veces permite usar hilo o pegamento para unir las piezas, mientras que el origami modular puro no usa elementos externos; las piezas se encajan entre sí.
Existe un estilo chino llamado "origami 3D" donde se juntan muchas piezas para crear modelos elaborados. A veces se usan billetes para hacer los módulos.
Plegado en Húmedo
El plegado en húmedo es una técnica de origami que permite crear modelos con curvas suaves en lugar de pliegues rectos y superficies planas. Consiste en humedecer el papel para que sea más fácil de moldear. Cuando el modelo se seca, mantiene su forma. Esta técnica es útil para crear animales con una apariencia muy natural. Otra forma de hacerlo es aplicar una capa de metilcelulosa al papel y dejarla secar. Luego, se humedece el modelo con agua para darle la forma final.
Origami Pureland
Este estilo requiere mucho cuidado y técnica. Solo se permite hacer un pliegue a la vez, y no se permiten pliegues más complejos como los invertidos. Todos los pliegues deben tener ubicaciones directas. Fue desarrollado por John Smith en los años 70 para ayudar a principiantes o a personas con dificultades motoras. A algunos diseñadores también les gusta el desafío de crear buenos modelos con estas reglas estrictas.
Teselados o Teselaciones
Esta rama del origami ha ganado popularidad recientemente, pero tiene una larga historia. Un teselado es un patrón de figuras que cubre una superficie plana sin dejar huecos ni superponerse. Los teselados de origami se hacen con papel, pero se pueden usar otros materiales que mantengan el pliegue.
Fujimoto, uno de los primeros maestros japoneses del origami, publicó libros con teselados. En los años 60, Ron Resch exploró mucho esta técnica. Artistas como Chris Palmer han creado teselados de origami detallados usando seda. Robert Lang y Alex Bateman usan programas de computadora para diseñar teselados. El primer libro estadounidense sobre el tema fue publicado por Eric Gjerde, y la primera convención internacional se realizó en Brasilia en 2006.
Origami Clásico
El origami clásico consiste en obtener figuras a partir de una hoja cuadrada de papel, sin usar tijeras ni pegamento.
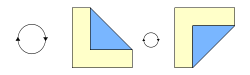
Dobleces
| Símbolos para dobleces básicos | |||||||||
|
|||||||||
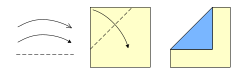
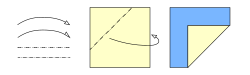
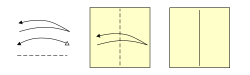
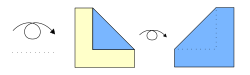
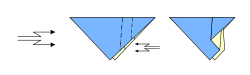
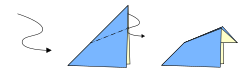
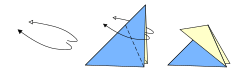
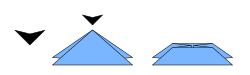
Una figura de origami se forma con dos tipos de dobleces:
- Valles: Son dobleces que se hunden en el papel.
- Montes: Son dobleces que sobresalen, como una montaña.
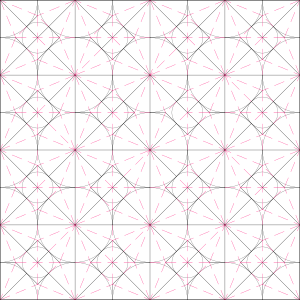
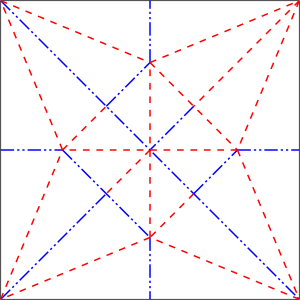
Cuando desdoblas una figura terminada, el patrón de valles y montes que queda se llama CP (Crease Pattern). A menudo, los diseñadores crean primero el CP y luego las instrucciones paso a paso.
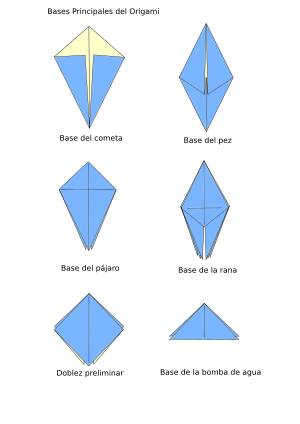
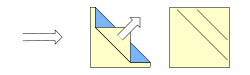
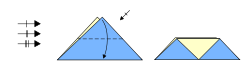
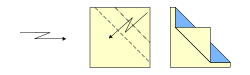
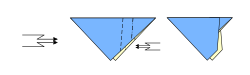
Bases
Tradicionalmente, hay cuatro bases clásicas que se hacen a partir de una hoja de papel cuadrada:
- La base del cometa: De donde se crea la figura del cisne.
- La base del pez: De ella surge un pez.
- La base del pájaro: La grulla es un ejemplo que la usa.
- La base de la rana: Que da como resultado la rana.
A estas se añaden otras dos bases sencillas:
- La base bomba de agua: De ella sale el globo de papel que se infla.
- El doblez preliminar (del inglés Preliminar fold).
Hoy en día, hay miles de bases, ya que la tendencia es diseñar una base específica para cada figura. Las seis bases mencionadas pueden usarse para crear partes adicionales en diseños más complejos. Por ejemplo, la base del pájaro se usa para aves porque tiene cuatro solapas que pueden convertirse en cabeza, cola y dos alas.
Diagramas
Hay dos formas principales de enseñar a otros cómo doblar una figura. El primer sistema, inventado por Yoshizawa, Harbin y Randlett, muestra todos los pasos uno por uno, desde el papel sin doblar hasta la figura terminada. El otro sistema es el Crease Pattern (CP), que muestra los dobleces principales de la figura en el papel sin doblar. Es popular entre los origamistas avanzados porque es una forma rápida de compartir sus diseños.
Sistema Yoshizawa-Harbin-Randlett
Este sistema usa líneas y flechas para indicar las instrucciones y la secuencia de doblado. Fue creado por Yoshizawa y popularizado por Harbin y Randlett. Aunque es muy cómodo para el que aprende, en los últimos 10 años, los artistas expertos han empezado a usar más los CP. Sin embargo, es difícil descifrar la secuencia de doblado y lograr el modelo final solo con un CP.
| Simbología origami | ||||||||||||||||||||||||
|
||||||||||||||||||||||||
CP (Crease Pattern)
Un CP (del inglés Crease Pattern, 'patrón de pliegue') es un diagrama que muestra la mayoría de los pliegues de un modelo final en una sola imagen. Es muy útil para figuras complejas, donde hacer instrucciones paso a paso sería demasiado trabajo. Se originó con diseñadores como Neal Elías, quien los usaba para guardar sus modelos. Hoy en día, la mayoría de los modelos muy complejos solo vienen con un CP.
Diseño de Figuras
Tipos de Pliegue
- Pliegues axiales: Son los que quedan alineados con el eje de simetría del modelo final.
- Pliegues bisagra: Son los pliegues que separan una solapa o apéndice de otra en la figura terminada.
- Pliegues cresta o cima: Suelen estar en el contorno de la base terminada.
Estos conceptos son independientes de las técnicas de diseño.
Técnicas de Diseño
Todas las técnicas de diseño se enfocan en la figura desdoblada, es decir, la hoja cuadrada con todos los dobleces de valles y montes marcados, lo que se llama crease pattern.
Existen muchas técnicas de diseño, la mayoría inventadas en los últimos 50 años. Robert Lang las clasifica así:
- División de puntas: Consiste en dividir una solapa en dos o más. Es útil para crear dedos en patas o manos de seres vivos, aunque las solapas resultantes son más cortas.
- Injerto: Consiste en añadir características a una base principal. Por ejemplo, se añaden cuadrados más pequeños a las esquinas de un cuadrado principal para crear una base final más compleja.
- Injerto de patrones: A un modelo básico se le añade un patrón que se repite muchas veces, como escamas en peces o dragones.
- Mosaico: Se descompone la figura en bloques básicos, como triángulos con dobleces internos. La idea es ver el papel como varias unidades flexibles que pueden separarse o unirse.
- Empaquetamiento de círculos: Para diseñar una figura, primero se cuenta cuántas solapas tendrá (por ejemplo, un perro tiene cabeza, cola y cuatro patas, es decir, seis solapas). Luego, se dibujan círculos en el papel cuadrado, uno por cada solapa, sin que se superpongan. Después se conectan los centros de los círculos con dobleces y se añaden dobleces secundarios. Esto crea una base para la figura, a la que luego se le añaden los detalles.
- Moléculas: Son polígonos (triángulos, cuadriláteros, pentágonos) que, al unirse, aseguran que la figura se pueda doblar y colapsar correctamente.
- Teoría del árbol: Se basa en dibujar la figura final como un árbol con ramas, donde cada rama es una solapa. Esto luego se traduce en círculos y "ríos" (partes sin doblar) en la hoja de papel.
- Pliegue en grilla cuadriculada (box pleating): Consiste en organizar cuadrados y rectángulos dentro del papel. El CP se llena de líneas verticales y horizontales, con ángulos de 45° y 90°. Es una técnica popular porque simplifica el diseño, aunque usa el papel de forma menos eficiente que el empaquetamiento de círculos. Muchos insectos y figuras humanas usan esta técnica.
- Pliegue en grilla hexagonal (Hex pleating): Técnica de plegado de hexágonos. Busca combinar lo mejor del empaquetamiento de círculos y rectángulos. Los ángulos de los pliegues son siempre múltiplos de 30°.
Las dos últimas técnicas pertenecen a una corriente de diseño llamada "empaquetamiento de polígonos".
Matemáticas en el Origami
El origami tiene una parte científica muy interesante. Los dobleces son operaciones de simetría que pueden estudiarse con la geometría. El aspecto matemático del origami no está reñido con el artístico. Por ejemplo, hay personas que demuestran teoremas geométricos usando solo papel y dobleces. Incluso se han publicado trabajos sobre cómo resolver ecuaciones complejas doblando papel.
El origami es una herramienta excelente para enseñar matemáticas, especialmente a nivel preuniversitario. Además, fomenta la curiosidad científica, ya que, al igual que las matemáticas, el origami es infinito.
En los últimos 30 años, ha habido grandes avances en el plegado de figuras gracias a artistas con conocimientos matemáticos. Ellos han creado teoremas y técnicas para diseñar de la forma más eficiente posible. Al principio, los artistas diseñaban por experiencia, pero ahora se puede usar una metodología específica con la ayuda de teoremas que indican qué es posible hacer.
Se han realizado muchos estudios matemáticos sobre el arte de doblar papel. Se ha investigado cómo se puede aplastar una figura de papel sin dañarla (problema conocido como flat-foldability) y cómo usar los dobleces para resolver ecuaciones matemáticas.
Se ha demostrado que algunos problemas de geometría clásica, como dividir un ángulo en tres partes iguales o duplicar el volumen de un cubo, no se pueden resolver con regla y compás, pero sí con unos pocos dobleces de papel. Se pueden resolver ecuaciones de hasta cuarto grado y ecuaciones polinomiales doblando papel (los axiomas de Huzita-Hatori son una contribución importante en este campo).
El problema del origami rígido, que trata los pliegues como líneas que unen dos superficies planas y rígidas, tiene gran importancia práctica. Por ejemplo, el pliegue de mapa de Miura es un pliegue rígido que se ha usado para desplegar grandes paneles solares en satélites espaciales.
Algunos de los teoremas más conocidos son:
- Teorema de Maekawa: Dice que la diferencia entre el número de montes y valles para lograr una superficie plana siempre debe ser 2.
- Teorema de Kawasaki: La suma de todos los ángulos alternos alrededor de un punto formado por pliegues debe ser 180 grados.
También existen axiomas relacionados con la geometría del origami, definidos por Humiaki Huzita, basados en 6 dobleces básicos, a los que se añadió un séptimo axioma:
- Axioma 1: Dados dos puntos P y Q, se puede hacer un pliegue que los une.
- Axioma 2: Dados dos puntos P y Q, se puede hacer un pliegue que lleva P sobre Q.
- Axioma 3: Dado un punto P y una línea r, se puede hacer un pliegue perpendicular a r que pasa por P.
- Axioma 4: Dadas dos líneas r y s, se puede hacer un pliegue que sitúe r sobre s.
- Axioma 5: Dados dos puntos P y Q y una línea r, podemos hacer un pliegue que sitúe P sobre r y pase por Q.
- Axioma 6: Dados dos puntos P y Q y dos líneas r y s, se puede hacer un pliegue que sitúe P sobre r y Q sobre s.
- Axioma 7: Dado un punto P y dos líneas r y s, se puede hacer un doblez perpendicular a r que coloca el punto P sobre la línea s.
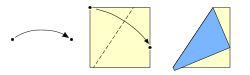
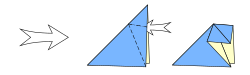
El Teorema de Haga permite encontrar fácilmente la tercera parte de una hoja de papel doblando una esquina inferior derecha hacia la mitad del borde superior del cuadrado.
Además de crear sus propias reglas geométricas, el origami es una herramienta educativa importante. Ayuda a mejorar la concentración, la memoria, el análisis y el desarrollo de conceptos geométricos, activando el pensamiento lógico-espacial y las habilidades motoras finas.
Papel para Origami
En el origami tradicional, que usa una sola hoja de papel cuadrada sin tijeras ni pegamento, el tipo de papel es muy importante, especialmente para modelos complejos. Cada persona que dobla papel debe buscar el tipo de papel con el que se sienta más cómoda. A menudo, se encuentran diferentes papeles adecuados para distintos tipos de figuras. En general, se recomienda que el papel tenga fibras largas y uniformes, lo que ayuda a que no se rompa fácilmente.
Una de las principales dificultades para los principiantes es usar papel pequeño (10x10 cm). Es mejor empezar con un tamaño mínimo de 20x20 cm. Las figuras complejas pueden requerir papeles muy grandes, de hasta 1 metro por 1 metro. El tipo de papel y la experiencia son fundamentales.
Tipos de Papel
Los papeles más valorados y que resisten más dobleces suelen tener fibras largas. Esto se nota al romper el papel: cuanto más largas sean las fibras, mejor será para doblar. Otro criterio es el gramaje del papel (gramos por metro cuadrado). Las figuras con muchas capas y dobleces son difíciles de hacer con papeles de más de 20 gramos. Los papeles más gruesos (40 gramos) suelen ser útiles para el plegado en húmedo.
Algunos tipos de papel populares son:
- Origamido: Una marca de papel muy especial y costosa, fabricada en Origamido Studio. Se hace a pedido con fibras vegetales específicas y pigmentos naturales.
- O-gami: Otra marca de papel artesanal, conocida por sus excelentes características para doblar. Es una alternativa al Origamido.
- Tant: Una marca de papel con muchas gamas de colores, ligeramente grueso y a veces usado en plegado en húmedo.
- Washi: Es el nombre del papel japonés tradicional, hecho de la corteza de arbustos como el kozo, gampi y mitsumata.
- Lokta: Papel hecho a mano en Nepal.
- Papel sándwich: Un papel artesanal con una capa de papel seda, una hoja de aluminio en el medio y otra capa de papel seda.
- Papel de envolver: El papel que se usa para envolver zapatos o camisas. Es útil para figuras complejas por sus 20 gramos por metro y gran resistencia.
- Papel kraft: También muy resistente al doblado por sus fibras largas, usado a menudo para practicar.
Programas para Diseño y Diagramas
Existen algunos programas de computadora que ayudan en el diseño y la creación de diagramas de origami:
- TreeMaker: Creado por Robert Lang, se enfoca en el diseño de figuras. Crea el patrón de pliegues (CP) y muestra qué partes del papel se convertirán en la cola, patas o cabeza de un animal.
- OriPa: Un programa para dibujar CP (crease patterns). Permite ver cómo se verá el CP una vez doblado y tiene una interfaz fácil de usar.
- Doodle: Usa código para generar diagramas de origami. El resultado es elegante, pero puede ser difícil de usar.
- Foldinator: Un programa en desarrollo para diseñar diagramas en línea.
Personajes Importantes en el Mundo del Origami
En el siglo XX, el origami tuvo un gran renacimiento con Akira Yoshizawa. Él inventó nuevas figuras e innovó con el plegado en húmedo. De él surgió una nueva corriente artística de diseño, a la que luego se sumaría la matemática.
Otros personajes importantes que han demostrado teoremas que llevan su nombre son: Humiaki Huzita, Jun Maekawa, Toshikazu Kawasaki, Robert Lang, Shuzu Fujimoto y Chris Palmer.
Robert Lang, ingeniero eléctrico y doctor en física aplicada, ha desarrollado el origami computacional, que usa algoritmos para doblar figuras. Actualmente, el Dr. Lang trabaja en proyectos que conectan el origami con problemas de ingeniería. Su libro Origami design secrets es una excelente guía para aprender a diseñar figuras nuevas y mejorar las existentes.
Mucha gente conoce el origami por los avioncitos o barquitos de papel. La idea de hacer avioncitos surgió cuando varios expertos intentaron crear una figura de papel que volara o se mantuviera en el aire. Esto se logró con éxito y es una forma en que el origami se ha transmitido de padres a hijos. Más allá del entretenimiento, los modelos de aviones de papel han ayudado a estudiar el comportamiento del viento, la influencia del peso y otros factores que mejoraron las técnicas de vuelo y la ingeniería aeronáutica.
En muchos países, los artistas del origami trabajan en proyectos para publicidad, páginas web de empresas, o como profesores que conectan el origami con otras materias.
El origami es un arte hermoso y complejo con una historia fascinante. Te invitamos a tomar una hoja de papel y experimentar la maravillosa sensación de crear, como dijo Katsushika Hokusai: «Un mago es capaz de convertir las hojas de papel en pájaros».
Origami y la Educación
El Origami en la Pedagogía
El origami es una gran ayuda en la educación, ofreciendo muchos beneficios y cualidades a quienes lo practican, ya sean estudiantes o cualquier persona. Aunque pocos educadores lo saben, el doblado de papel ha sido una herramienta en las escuelas desde el siglo XIX. Algunos de sus beneficios son:
- Desarrolla la destreza, exactitud y precisión manual, requiriendo atención y concentración.
- Crea motivación personal para desarrollar la creatividad y la coordinación entre lo real y lo abstracto.
- Anima a los estudiantes a crear sus propios modelos.
- Ofrece momentos de diversión y relajación.
- Fortalece la autoestima a través de la creación de figuras propias.
Si se fomenta el trabajo manual en los niños desde pequeños, desarrollarán habilidades artísticas y la capacidad de ubicar objetos en el espacio, algo que muchos niños no pueden hacer si no se potencia el trabajo manual en sus primeros años.
Es ideal que los niños comiencen una actividad manual a edad temprana, ya que se ha demostrado que el entrenamiento de los dedos de un bebé acelera la maduración del cerebro. Ejercitar el movimiento de los dedos de ambas manos es una base para el desarrollo bilateral del cerebro y el avance intelectual, aprovechando que el cerebro está en su mayor capacidad de aprendizaje.
El trabajo de coordinación de ambas manos, la actividad de la inteligencia y la atención son necesarias en el origami. Este arte requiere memoria, imaginación y pensamiento. Al usar activamente las manos, se produce un masaje natural en las puntas de los dedos, lo que beneficia el equilibrio de los procesos cerebrales. El origami, al ser un arte para ambas manos, ofrece una satisfacción creativa y puede ser un apoyo en la formación integral de las personas, ayudándoles a comunicarse y a interactuar con los demás.
El Origami en la Psicología
El origami también ha demostrado ser útil en el ámbito de la psicología. Se ha comprobado que concentrarse en una actividad manual ayuda a liberar tensiones y estimula los procesos mentales, lo que puede alejar a una persona de sus preocupaciones.
En algunas universidades, se realizan estudios con estudiantes que tienen dificultades de atención, y se les estimula con el doblado de papel. En un hospital de Cali, Colombia, este arte se usa en el tratamiento de niños con problemas emocionales, como dificultades de atención, expresión e hiperactividad.
El origami, usado como herramienta o terapia, permite compartir sentimientos y conocimientos, ayuda a resolver problemas, facilita la comunicación no verbal, establece metas, ofrece un acercamiento seguro y brinda apoyo psicológico. También es una oportunidad para disfrutar y descubrir un futuro pasatiempo, entre otras experiencias que se viven al aplicar el origami en la rehabilitación.
Variantes del Origami
- Kusudama
- Pepakura
- Kirigami
- Makigami
Véase también
 En inglés: Origami Facts for Kids
En inglés: Origami Facts for Kids
- Avión de Papel
- Adivinador de papel
- Mil Grullas de Papel
- Zen
- Kushiro Hatori
- Topología
- Teoría de los nudos
- Akira Yoshizawa