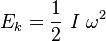Volante de inercia para niños
Un volante de inercia es una pieza mecánica que ayuda a mantener un movimiento suave y constante en las máquinas. Imagina una rueda pesada que, una vez que empieza a girar, sigue haciéndolo por sí misma, incluso si la fuerza que la impulsaba se detiene por un momento. Esto se debe a la inercia, que es la tendencia de los objetos a mantener su estado de movimiento.
El volante de inercia almacena energía de movimiento (energía cinética) y la libera cuando es necesario. Así, evita que la velocidad de giro cambie bruscamente, haciendo que el flujo de energía sea más uniforme entre la fuente de potencia y lo que esta mueve.
En los coches, el volante de inercia es muy importante. Se conecta al cigüeñal (una pieza que transforma el movimiento de los pistones en giro) y al embrague. Su trabajo es ayudar a que el giro del motor sea regular y transmitir ese movimiento a la caja de cambios y, finalmente, a las ruedas.
Hoy en día, se investigan nuevas formas de usar los volantes de inercia:
- Pueden guardar la energía que se produce al frenar un vehículo para usarla después al acelerar, como en el sistema KERS de algunos coches de carreras.
- Ayudan a que las instalaciones que generan electricidad con energía eólica funcionen de manera más estable.
- En los trenes eléctricos, que ya recuperan energía al frenar, los nuevos diseños de volantes de inercia pueden hacer que este proceso sea aún más eficiente.

Contenido
¿Cómo funciona un volante de inercia?
Un volante de inercia funciona gracias a principios de la física. Su capacidad para almacenar energía depende de su masa, su forma y la velocidad a la que gira. Cuanto más pesado y más rápido gire, más energía podrá guardar.
Energía almacenada en un volante
La energía que un volante puede almacenar se llama energía cinética de rotación. Se calcula con una fórmula que considera qué tan difícil es cambiar su movimiento de giro (su momento de inercia) y qué tan rápido está girando (su velocidad angular).
| Símbolo | Significado |
|---|---|
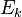 |
Energía de movimiento (cinética) |
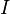 |
Momento de inercia (resistencia a cambiar el giro) |
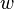 |
Velocidad angular (qué tan rápido gira) |
Para entender mejor el momento de inercia, piensa que es más fácil girar una regla por su centro que por uno de sus extremos. Esto se debe a cómo se distribuye su masa.
Comportamiento del volante
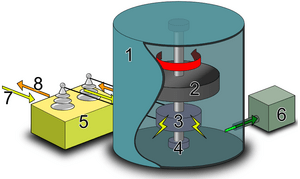
El volante de inercia recibe energía de una fuente (como un motor) y la entrega a una carga (como las ruedas de un coche). Cuando la fuente de energía no es constante, el volante ayuda a que la entrega de energía sea más suave. Por ejemplo, en un motor de coche, las explosiones de combustible no son continuas, pero el volante de inercia asegura que el giro del cigüeñal sea uniforme.
Materiales modernos para volantes
La cantidad de energía que un volante puede almacenar de forma segura depende de lo fuerte que sea el material del que está hecho. Si el volante gira demasiado rápido, las fuerzas pueden hacer que se rompa.
La resistencia del material a estirarse o romperse es muy importante. Los materiales que son muy resistentes y ligeros son los mejores para los volantes de inercia. Por eso, la fibra de carbono es un material muy interesante para fabricar volantes de inercia modernos, ya que es muy fuerte y ligera a la vez.
¿Por qué son necesarios los volantes de inercia?
Los volantes de inercia son esenciales en muchas máquinas porque la energía que producen no siempre es constante. Por ejemplo, en un motor de coche, las explosiones de combustible ocurren en momentos específicos, no de forma continua. El volante de inercia ayuda a suavizar esos impulsos de energía, asegurando un movimiento de giro constante y sin tirones. Esto es clave para que máquinas como las locomotoras de vapor o los motores de los coches funcionen bien.
Diseño de un volante de inercia
Generalmente, un volante de inercia es una rueda o un disco grande y pesado, hecho de materiales como fundición o acero. Se conecta al eje del motor y sus dimensiones se calculan cuidadosamente para que funcione perfectamente con la máquina de la que forma parte. En algunos aviones, la propia hélice actúa como volante de inercia.
Usos comunes de los volantes de inercia
Los volantes de inercia se encuentran en muchos lugares, algunos de ellos son:
- En los platos de los tocadiscos antiguos, para que giren a una velocidad constante.
- En algunos sistemas de energía de respaldo (llamados sistemas de alimentación ininterrumpida), para almacenar energía y usarla si se va la luz.
- En juguetes, como algunos coches de juguete, para darles impulso.
- En las prensas mecánicas, para acumular la energía necesaria para golpear o presionar con fuerza.
Ver también
- Freno regenerativo
- Batería inercial
- Girobús
- Giróscopo
- Vehículo híbrido
- Condensador
- Inductor
- Volante bimasa
Véase también
 En inglés: Flywheel Facts for Kids
En inglés: Flywheel Facts for Kids