Suma de Riemann para niños
En matemáticas, la Suma de Riemann es una forma de calcular el área aproximada debajo de una curva o de una función. Imagina que quieres saber cuánto espacio hay debajo de una línea curva en un gráfico. Como no es una forma simple como un cuadrado o un círculo, no puedes usar una fórmula directa.
Para resolver esto, el matemático alemán Bernhard Riemann (del siglo XIX) propuso una idea: dividir el área bajo la curva en muchas formas más sencillas, como rectángulos. Luego, calculas el área de cada uno de esos rectángulos y los sumas todos. El resultado será una aproximación del área total.
Cuanto más pequeños y numerosos sean los rectángulos que uses, más precisa será tu aproximación. Si haces los rectángulos infinitamente pequeños, la suma se acercará mucho al área exacta, que es lo que se calcula con una integral.
Contenido
¿Qué es una Suma de Riemann?
Una Suma de Riemann es una técnica para estimar el área bajo una curva en un gráfico. Para hacer esto, se divide el espacio debajo de la curva en varias secciones. En cada sección, se dibuja una figura geométrica simple, como un rectángulo. La altura de cada rectángulo se elige de una manera específica, y su ancho es el tamaño de la sección.
Después de dibujar todos los rectángulos, se calcula el área de cada uno. Finalmente, se suman todas esas áreas para obtener una estimación del área total bajo la curva.
¿Por qué usamos las Sumas de Riemann?
Las Sumas de Riemann son muy útiles porque nos permiten encontrar el área de formas complejas que no tienen una fórmula sencilla. Por ejemplo, si tienes una función que describe el movimiento de un objeto, el área bajo su curva de velocidad te dirá la distancia total recorrida.
Aunque la suma de Riemann es una aproximación, es una herramienta fundamental en el cálculo integral. Nos ayuda a entender cómo se calcula el área exacta cuando los rectángulos se vuelven infinitamente pequeños.
Tipos de Sumas de Riemann
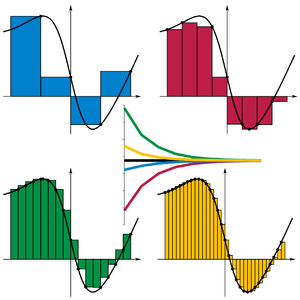
Existen diferentes maneras de elegir la altura de los rectángulos, lo que da lugar a distintos tipos de Sumas de Riemann. Cada método puede dar una aproximación ligeramente diferente, pero todos se acercan al valor real a medida que los rectángulos se hacen más pequeños.
Para estos métodos, el intervalo que estamos midiendo se divide en 'n' partes iguales. Cada una de estas partes tiene un ancho que llamamos `Δx`.
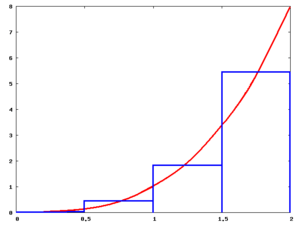
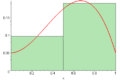
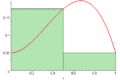
Suma de Riemann por la izquierda
En este método, la altura de cada rectángulo se toma del punto más a la izquierda de cada sección. Es decir, si tienes una sección que va de un punto A a un punto B, la altura del rectángulo se basa en el valor de la función en el punto A.
Si la curva está bajando (disminuye), esta suma tiende a sobreestimar el área. Si la curva está subiendo (aumenta), tiende a subestimar el área.
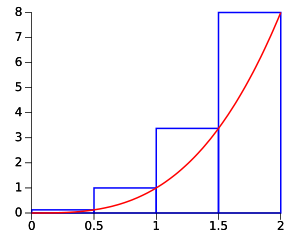
Suma de Riemann por la derecha
Aquí, la altura de cada rectángulo se toma del punto más a la derecha de cada sección. Si la sección va de A a B, la altura del rectángulo se basa en el valor de la función en el punto B.
Si la curva está bajando, esta suma tiende a subestimar el área. Si la curva está subiendo, tiende a sobreestimar el área.
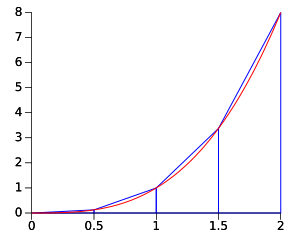
La Regla del Punto Medio
Con este método, la altura de cada rectángulo se calcula usando el valor de la función en el punto medio de cada sección. Por ejemplo, si una sección va de A a B, se toma el punto que está justo a la mitad entre A y B para determinar la altura.
Este método suele dar una aproximación más precisa que las sumas por la izquierda o por la derecha, porque "equilibra" los errores.
Suma Trapezoidal
Aunque no usa rectángulos, la suma trapezoidal es muy similar a las Sumas de Riemann. En lugar de rectángulos, se usan trapecios para aproximar el área. Un trapecio tiene dos lados paralelos y dos no paralelos. En este caso, los lados paralelos son las alturas de la función en los extremos izquierdo y derecho de cada sección.
El área de un trapecio se calcula como el promedio de las dos alturas multiplicado por el ancho de la base. Curiosamente, la suma trapezoidal es igual al promedio de la suma de Riemann por la izquierda y la suma de Riemann por la derecha.
¿Cómo se relaciona con el Cálculo?
Las Sumas de Riemann son el punto de partida para entender el concepto de integral definida en el cálculo. Una integral definida es la forma exacta de calcular el área bajo una curva.
Imagina que haces los rectángulos de tu Suma de Riemann cada vez más y más delgados, y que usas un número infinito de ellos. A medida que el ancho de cada rectángulo se acerca a cero y el número de rectángulos se vuelve infinito, la suma de sus áreas se acerca al valor exacto de la integral.
Esto significa que la integral es el "límite" de la Suma de Riemann cuando la división se hace infinitamente fina. Las animaciones a continuación muestran cómo la aproximación mejora a medida que se usan más rectángulos:
Galería de imágenes
Véase también
 En inglés: Riemann sum Facts for Kids
En inglés: Riemann sum Facts for Kids
- Integración de Riemann
- Integral de Darboux


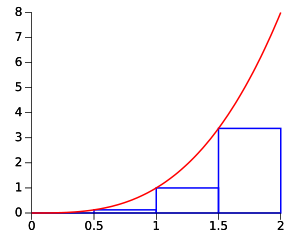
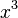 sobre [0,2] usando 4 subdivisiones
sobre [0,2] usando 4 subdivisiones