Regresión logística para niños
En estadística, la regresión logística es una herramienta especial que nos ayuda a predecir la probabilidad de que algo suceda o no. Imagina que quieres saber si un evento ocurrirá (como "sí" o "no", "verdadero" o "falso"). La regresión logística usa información que ya conocemos para calcular esa probabilidad.
Por ejemplo, si queremos predecir si una persona comprará un producto, podemos usar datos como su edad, ingresos o si ya compró algo similar antes. La regresión logística nos da una probabilidad, como un porcentaje, de que esa persona compre el producto.
Esta herramienta es muy útil en campos como la medicina y las ciencias sociales. A veces se le llama modelo logístico o modelo logit.
Contenido
¿Qué es la regresión logística?
La regresión logística es un tipo de análisis de regresión que se usa cuando el resultado que queremos predecir es una variable categórica. Esto significa que el resultado solo puede ser una de un número limitado de opciones, como "sí" o "no", "aprobado" o "reprobado", "enfermo" o "sano".
¿Cómo funciona la regresión logística?
Imagina que tienes un grupo de semillas y quieres saber cuántas germinarán. Puedes plantar varias semillas (digamos, n semillas) y observar cuántas de ellas crecen. La regresión logística nos ayuda a entender qué factores (como la cantidad de agua o la temperatura) influyen en la probabilidad de que una semilla germine.
En lugar de predecir un número exacto (como en la regresión lineal), la regresión logística predice una probabilidad. Esta probabilidad siempre estará entre 0 y 1 (o entre 0% y 100%). Por ejemplo, una probabilidad de 0.8 significa que hay un 80% de posibilidades de que el evento ocurra.
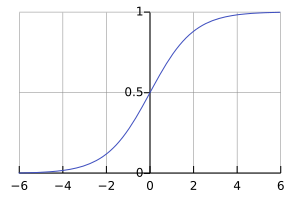
La función logística: una curva en forma de "S"
La regresión logística utiliza una fórmula especial llamada "función logística". Esta función crea una curva en forma de "S" cuando la dibujamos en un gráfico. Esta curva es perfecta para representar probabilidades, porque empieza cerca de 0, sube suavemente y termina cerca de 1.
La curva en "S" nos ayuda a ver cómo la probabilidad de un evento cambia a medida que los factores que lo influyen aumentan o disminuyen. Por ejemplo, si estudias más para un examen, la probabilidad de aprobar aumenta, pero no de forma lineal, sino siguiendo esta curva. Al principio, un poco de estudio hace una gran diferencia, pero después de cierto punto, estudiar mucho más no aumenta tanto la probabilidad.
¿Para qué se usa la regresión logística?
La regresión logística se utiliza en muchos campos para tomar decisiones importantes.
- Medicina: Para predecir la probabilidad de que un paciente desarrolle una enfermedad basándose en su edad, hábitos o historial médico.
- Economía: Para predecir si un cliente pagará un préstamo a tiempo o si una empresa tendrá éxito.
- Marketing: Para saber si un cliente hará clic en un anuncio o comprará un producto.
- Ciencias sociales: Para entender qué factores influyen en las decisiones de las personas, como votar por un candidato.
Ejemplos sencillos de regresión logística
Imaginemos que queremos predecir si un estudiante aprobará un examen basándonos en las horas que estudió.
Si un estudiante estudió 50 horas, y la regresión logística nos dice que la probabilidad de aprobar es de 2/3 (aproximadamente 67%), esto significa que es dos veces más probable que apruebe a que no apruebe. Es como decir que las "posibilidades" de aprobar son de 2 a 1.
La regresión logística nos ayuda a entender la relación entre las horas de estudio y la probabilidad de éxito, dándonos una idea clara de las posibilidades.
Extensiones de la regresión logística
A veces, el resultado que queremos predecir no es solo "sí" o "no", sino que tiene más de dos categorías. Por ejemplo, si queremos predecir si un cliente comprará un producto A, B o C. Para estos casos, existen extensiones de la regresión logística:
- Regresión logística multinomial: Se usa cuando el resultado tiene tres o más categorías que no tienen un orden específico (como colores: rojo, azul, verde).
- Regresión logística ordinal: Se usa cuando el resultado tiene tres o más categorías que sí tienen un orden (como calificaciones: bajo, medio, alto).
Estas extensiones hacen que la regresión logística sea aún más versátil para analizar diferentes tipos de datos y hacer predicciones útiles.
Véase también
 En inglés: Logistic regression Facts for Kids
En inglés: Logistic regression Facts for Kids
- Red neuronal artificial
- Minería de datos
- Análisis discriminante lineal
- Perceptrón