Análisis de la regresión para niños
En estadística, el análisis de la regresión es una herramienta muy útil para entender cómo una cosa (una variable) se relaciona con otra. Imagina que quieres saber si la edad de una persona influye en cuánto dinero gana. Con la regresión, puedes encontrar una conexión entre la edad y el salario.
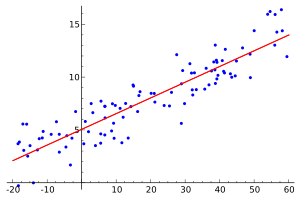
En pocas palabras, la regresión es como dibujar una línea en un gráfico. Esta línea nos muestra la tendencia general entre dos grupos de datos. Por ejemplo, si dibujamos una línea de regresión para la edad y el salario, podríamos ver cómo el salario tiende a aumentar a medida que la gente se hace mayor.
Los expertos en datos usan la regresión para entender estas relaciones y, a veces, para predecir cosas en el futuro. Si sabemos la edad de alguien, podríamos usar esta línea para estimar su salario, basándonos en lo que hemos visto en otras personas.
El análisis de regresión incluye muchas formas de estudiar cómo una variable principal (la que queremos entender) se ve afectada por una o más variables que la influyen. Nos ayuda a ver cómo cambia el valor de la variable principal cuando cambiamos el valor de una de las variables que la influyen, manteniendo las demás sin cambios.
Generalmente, el análisis de regresión busca el valor promedio de la variable principal cuando las variables que la influyen están fijas. El objetivo es encontrar una "función de regresión", que es como una fórmula que describe esta relación. También nos interesa saber cuánto varían los datos alrededor de esta función.
El análisis de regresión se usa mucho para hacer predicciones y pronósticos. Es una de las primeras herramientas que se aprenden en el campo del aprendizaje automático por lo sencilla que es. También sirve para descubrir cuáles de las variables que influyen son importantes y cómo se relacionan. A veces, puede ayudar a entender si una cosa causa otra, pero hay que tener cuidado, porque una conexión no siempre significa que una cosa sea la causa de la otra.
Se han creado muchas técnicas para hacer análisis de regresión. Algunas, como la regresión lineal, usan un número limitado de valores desconocidos que se calculan a partir de los datos. Otras, como la regresión no paramétrica, son más flexibles y no se limitan a un conjunto específico de funciones.
La efectividad de estos métodos depende de cómo se generaron los datos y de cómo se ajustan al método de regresión que se usa. Como no siempre sabemos cómo se generaron los datos, a menudo tenemos que hacer suposiciones. Si tenemos suficientes datos, a veces podemos verificar estas suposiciones. Los modelos de regresión pueden ser útiles para predecir, incluso si las suposiciones no son perfectas. Sin embargo, en algunos casos, especialmente con pocos datos o al buscar causas, los métodos de regresión pueden dar resultados que no son correctos.
Contenido
Historia del Análisis de Regresión
¿Cuándo Empezó el Análisis de Regresión?
La primera forma de regresión se llamó el método de mínimos cuadrados. Fue presentado por un científico llamado Legendre en 1805 y por Gauss en 1809. Ellos usaron este método para calcular las órbitas de los cuerpos celestes, como los cometas y los planetas, basándose en observaciones astronómicas. Gauss mejoró esta teoría en 1821.
¿De Dónde Viene la Palabra "Regresión"?
La palabra "regresión" fue usada por primera vez por Francis Galton en el siglo XIX. Él la usó para describir algo que observó en la biología: que los hijos de padres muy altos tendían a tener una altura más cercana al promedio general. A esto lo llamó "regresión hacia la media".
Al principio, para Galton, la regresión solo tenía este significado biológico. Pero más tarde, otros científicos como Udny Yule y Karl Pearson extendieron su trabajo a un campo más general de la estadística. Luego, Ronald Fisher hizo más avances en los años 1922 y 1925, haciendo que la técnica fuera aún más útil.
¿Cómo se Hacía Antes?
En los años 1950 y 1960, los economistas usaban calculadoras electromecánicas para hacer los cálculos de regresión. Antes de 1970, a veces se tardaba hasta 24 horas en obtener el resultado de un análisis de regresión. ¡Imagina cuánto tiempo tomaba!
Hoy en día, los métodos de regresión siguen siendo un área de estudio muy activa. En las últimas décadas, se han desarrollado nuevas formas de regresión para manejar datos más complejos, como series de tiempo, imágenes o datos con información faltante.
Componentes de un Modelo de Regresión
¿Qué Elementos Tiene un Modelo de Regresión?
Cuando los investigadores quieren usar el análisis de regresión, primero eligen un "modelo" que quieren estudiar. Luego, usan un método para calcular los valores de ese modelo. Los modelos de regresión suelen tener estos elementos:
- Valores desconocidos: Son números que no conocemos al principio y que queremos descubrir.
- Variables que influyen: Son los datos que observamos y que creemos que afectan a la variable principal.
- Variable principal: Es la que queremos entender o predecir.
- Errores: Son las diferencias que no podemos explicar con el modelo, como el ruido o cosas que no se tuvieron en cuenta.
La mayoría de los modelos de regresión sugieren que la variable principal es el resultado de una fórmula que usa las variables que influyen y los valores desconocidos, más un pequeño error.
El objetivo es encontrar la fórmula que mejor se ajuste a los datos. A veces, ya sabemos cómo se relacionan las variables. Si no, elegimos una forma sencilla o flexible para la fórmula. Por ejemplo, en una regresión simple, podríamos pensar que la variable principal es igual a un número fijo más otro número multiplicado por la variable que influye, más un error.
Una vez que se elige el modelo, los métodos de regresión nos ayudan a calcular los valores desconocidos. Por ejemplo, el método de Mínimos cuadrados busca los valores que hacen que la suma de los errores al cuadrado sea lo más pequeña posible. Con estos valores calculados, podemos predecir o ver qué tan bien el modelo explica los datos.
Es muy importante tener suficientes datos para poder calcular un modelo de regresión. Si no tenemos suficientes datos, podríamos encontrar muchas soluciones que parecen correctas, pero que en realidad no nos dan una respuesta única y útil. En general, para calcular un modelo con varios valores desconocidos, necesitamos tener al menos tantos puntos de datos como valores desconocidos. Además, las variables que influyen deben ser diferentes entre sí; no podemos crear una a partir de las otras.
Tipos de Modelos de Regresión
¿Qué es la Regresión Lineal Simple?
Este es un tipo de modelo de regresión que usa solo dos variables: una que influye (llamada X) y otra que es influida (llamada Y). Suponemos que la variable Y depende de la variable X.
Para la regresión lineal simple, se cree que X e Y se relacionan de una forma muy sencilla, como una línea recta. Hay algunos números desconocidos que se calculan para encontrar la mejor línea que represente esta relación. Estos números se llaman coeficientes de regresión y se pueden estimar con métodos como el de Mínimos cuadrados.
¿Qué es la Regresión No Lineal?
La Regresión no lineal se usa cuando la relación entre las variables no es una línea recta. En estos casos, la relación puede ser más compleja, como una curva. Un ejemplo es la Regresión segmentada, donde la relación cambia en diferentes partes de los datos.
Galería de imágenes
Véase también
 En inglés: Regression analysis Facts for Kids
En inglés: Regression analysis Facts for Kids