Proyección tridimensional para niños

La proyección tridimensional es un conjunto de técnicas que nos permiten mostrar objetos que tienen tres dimensiones (como una caja o una persona) en una superficie que solo tiene dos dimensiones (como una pantalla de computadora o una hoja de papel).

Piensa en cómo ves el mundo: los objetos que están lejos parecen más pequeños que los que están cerca. La proyección tridimensional busca recrear esa sensación o, en otros casos, mostrar los objetos de una manera que sea útil para el diseño y la construcción.

Esta técnica se usa mucho en el dibujo técnico, que es el tipo de dibujo que usan los ingenieros y arquitectos. También es una parte muy importante de los programas de computadora que crean gráficos en 3D, como los que ves en los videojuegos o en las películas animadas.

Proyección Ortográfica: Dibujos a Escala

Planta, alzado y perfil de un objeto tridimensional (proyecciones ortográficas según tres ejes ortogonales)

Representación axonométrica (proyección cilíndrica) del objeto anterior

Cuando miramos algo con nuestros ojos, los objetos lejanos se ven más pequeños. Sin embargo, la proyección ortográfica ignora este efecto. ¿Por qué? Porque su objetivo es crear dibujos donde las medidas sean exactas, sin importar la distancia. Esto es muy útil para la construcción y la ingeniería.

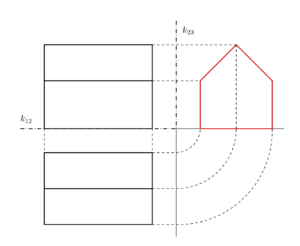
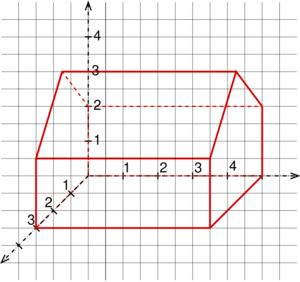
Las proyecciones ortográficas son como tomar fotos de un objeto desde diferentes ángulos, pero siempre de frente. Por ejemplo, puedes ver la "planta" (vista desde arriba), el "alzado" (vista desde el frente) o el "perfil" (vista desde un lado). Estas vistas nos permiten conocer las medidas precisas de un objeto tridimensional.

En este tipo de proyección, las longitudes de los objetos se mantienen a la misma escala, sin importar si están lejos o cerca del punto de vista. Esto significa que un objeto de 1 metro de largo siempre se verá de la misma longitud en el dibujo, ya sea que esté a 1 metro o a 100 metros de distancia en la realidad.

Proyección en Perspectiva: Como Vemos el Mundo

Diagrama de una transformación perspectiva

La perspectiva es la forma en que nuestros ojos ven el mundo: los objetos que están lejos parecen más pequeños que los que están cerca. A diferencia de la proyección ortográfica, la proyección en perspectiva sí muestra los objetos distantes más pequeños. Esto hace que las imágenes se vean mucho más realistas, como si las estuviéramos viendo en la vida real o a través de una cámara.

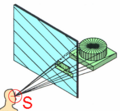
Para entender cómo funciona la proyección en perspectiva, puedes imaginar que estás mirando un objeto a través del visor de una cámara fotográfica. La posición de la cámara, hacia dónde apunta y qué tan amplio es su "campo de visión" (cuánto abarca la imagen) son factores que cambian cómo se ve el objeto proyectado.

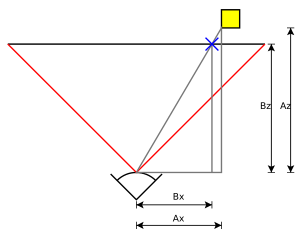
En esta proyección, para saber dónde aparecerá un punto de un objeto en la pantalla, se usa una idea sencilla: si un objeto está más lejos de la cámara, su imagen en la pantalla será más pequeña. Es como si trazaras líneas desde el objeto hasta el ojo de la cámara, y donde esas líneas cruzan una "pantalla imaginaria" es donde se dibuja el objeto.

Para calcular la posición de un punto en la pantalla (por ejemplo, su coordenada x), se puede usar una fórmula simple que relaciona la coordenada x del objeto, la distancia focal de la cámara (qué tan lejos está la "pantalla imaginaria" del centro de la cámara) y la distancia del objeto a la cámara.

Esta técnica es fundamental para crear imágenes y animaciones que se sientan muy reales, ya que imita la forma natural en que percibimos la profundidad y la distancia.

Galería de imágenes

• 

  Proyección de un objeto tridimensional sobre un plano

Véase también

En inglés: 3D projection Facts for Kids