Programación no lineal para niños
La programación no lineal (PNL) es una parte de las matemáticas que nos ayuda a encontrar la mejor solución para problemas donde lo que queremos lograr (el "objetivo") o las reglas que debemos seguir (las "restricciones") no son líneas rectas, sino curvas. Imagina que quieres encontrar el punto más alto o más bajo en una montaña, pero la montaña tiene muchas formas y no es una pendiente simple. La PNL busca ese punto óptimo.
Se usa para resolver problemas de optimización, que es como buscar la mejor manera de hacer algo. Por ejemplo, cómo gastar menos dinero o cómo producir más, pero cuando las relaciones entre las cosas no son simples y directas.
Contenido
¿Para qué sirve la programación no lineal?
La programación no lineal se usa en muchos campos para tomar decisiones importantes.
Optimización de costos de transporte
Imagina que una empresa necesita mover productos, como gasolina, usando diferentes medios: tuberías, camiones o barcos. Cada método tiene costos que no son fijos; por ejemplo, si usas una tubería, el costo por litro puede bajar mucho si transportas grandes cantidades. La PNL ayuda a encontrar la combinación más barata de transporte, considerando que los costos pueden cambiar de forma compleja.
Análisis de datos en experimentos
En la ciencia, cuando los investigadores recogen datos, a veces necesitan encontrar la mejor curva que se ajuste a esos datos. Por ejemplo, si estudian cómo se comporta un material, pueden tener un modelo teórico con valores que cambian. La PNL les ayuda a encontrar los valores que mejor explican lo que observaron en el experimento.
¿Cómo se plantea un problema de PNL?
Un problema de programación no lineal se puede entender como:
- Maximizar algo: Por ejemplo, las ganancias de una empresa.
- Minimizar algo: Por ejemplo, los costos de producción.
Siempre hay una función que representa lo que queremos maximizar o minimizar, y un conjunto de reglas o límites que debemos cumplir.
Tipos de soluciones posibles
Cuando intentamos resolver un problema de PNL, podemos encontrarnos con diferentes situaciones:
Problema inviable
Esto ocurre cuando no hay ninguna solución que cumpla con todas las reglas al mismo tiempo. Es como si te pidieran que dibujes un círculo cuadrado; simplemente no se puede. Las reglas se contradicen entre sí.
Problema factible
Significa que sí existe al menos una solución que cumple con todas las reglas. Hay una o más maneras de lograr lo que se pide.
Problema ilimitado
En este caso, el objetivo que queremos maximizar (o minimizar) puede mejorar infinitamente sin encontrar un límite. Por ejemplo, si quieres ganar dinero y no hay restricciones, podrías ganar una cantidad ilimitada. Esto significa que no hay una "mejor" solución única, porque siempre puedes encontrar una aún mejor.
¿Cómo se resuelven estos problemas?
Para resolver un problema de PNL, a menudo se transforma en un problema más sencillo. Una forma es dividir el área de búsqueda en partes más pequeñas y manejables.
Imagina dos pelotas en un canal que quieren llegar al punto más bajo posible, pero no pueden atravesarse. El objetivo es minimizar la energía de las pelotas. La regla es que no pueden chocar.
Aquí te explicamos algunas formas de manejar las reglas o restricciones:
- Multiplicadores de Lagrange: Es como si pusiéramos una "multa" si las reglas no se cumplen. Si las pelotas se acercan demasiado, se aplica una fuerza que las empuja para que no se toquen. Esta fuerza es el "multiplicador de Lagrange".
- Funciones de barrera: Aquí, las reglas se convierten en "paredes" que se hacen más fuertes a medida que te acercas a ellas. Si las pelotas intentan tocarse, es como si tuvieran un escudo que se vuelve más y más duro, impidiendo que se atraviesen.
- Funciones de penalización: Similar a las funciones de barrera, pero aquí se aplica una "penalización" si se rompe la regla. Si las pelotas se atraviesan un poco, se les aplica una fuerza que las empuja de vuelta a su posición correcta. Cuanto más se atraviesen, mayor es la penalización.
- Método de Lagrange aumentado: Combina las ideas de los multiplicadores de Lagrange y las funciones de penalización para ser más efectivo.
- Eliminar variables: A veces, si una regla es muy estricta, podemos simplificar el problema fijando algunas variables. Por ejemplo, si las pelotas no pueden penetrarse, podemos hacer que sus puntos de contacto sean iguales, eliminando la posibilidad de que se atraviesen.
Métodos para encontrar la solución
Si el problema es más simple (lineal), se usan métodos específicos. Pero para los problemas no lineales, se usan técnicas más avanzadas.
Si la función objetivo es "cóncava" (como una montaña con una cima) o "convexa" (como un valle con un fondo), y las reglas forman un espacio "convexo", se pueden usar métodos de optimización convexa.
Para problemas más complejos, existen métodos como:
- Ramificación y poda: Este método divide el problema grande en partes más pequeñas. Luego, se resuelven estas partes y se van descartando las que no llevan a una buena solución, hasta encontrar la mejor.
- Condiciones de Karush-Kuhn-Tucker: Son como una lista de verificación que nos dice si una solución es la mejor posible.
Algunos algoritmos que se usan para resolver estos problemas son:
- El método de Newton
- El método cuasi-Newton
- El método del gradiente conjugado
- La búsqueda lineal
- Las regiones de confianza
- El método Nelder-Mead
Ejemplos de problemas de PNL
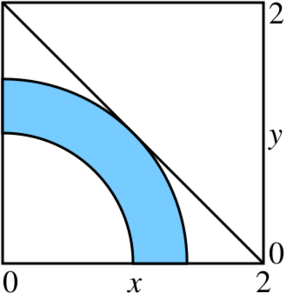
Ejemplo bidimensional
Imagina que tienes un área en un plano (como un mapa) definida por estas reglas:
- x₁ debe ser mayor o igual a 0
- x₂ debe ser mayor o igual a 0
- x₁² + x₂² debe ser mayor o igual a 1 (esto forma un círculo)
- x₁² + x₂² debe ser menor o igual a 2 (esto forma otro círculo más grande)
Y quieres encontrar el punto (x₁, x₂) dentro de esa área que haga que la suma x₁ + x₂ sea lo más grande posible.
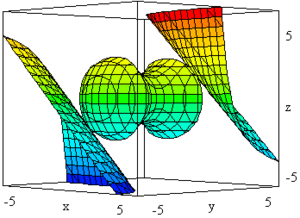
Ejemplo tridimensional
Ahora, imagina un espacio en 3D con estas reglas:
- x₁² − x₂² + x₃² debe ser menor o igual a 2
- x₁² + x₂² + x₃² debe ser menor o igual a 10
Y quieres encontrar el punto (x₁, x₂, x₃) dentro de ese espacio que haga que x₁x₂ + x₂x₃ sea lo más grande posible.
Usos de la programación no lineal
La PNL es una herramienta muy útil para resolver problemas de optimización en la vida real.
Gestión de la cadena de suministro
Las empresas usan la PNL para decidir cómo asignar sus recursos, cuándo producir y cómo distribuir sus productos. Los costos de transporte o almacenamiento pueden ser complejos y no lineales. La PNL ayuda a minimizar los costos totales mientras se cumplen las demandas.
Optimización de carteras
Los inversionistas quieren obtener el mayor beneficio posible con el menor riesgo. La relación entre el riesgo y el beneficio de una inversión no es lineal. La PNL ayuda a encontrar la mejor combinación de inversiones que cumpla con el presupuesto y la tolerancia al riesgo.
Optimización de sistemas energéticos
En la producción de energía, especialmente la renovable, la PNL se usa para encontrar la mejor combinación de fuentes de energía. La producción de energía solar o eólica depende de las condiciones del clima, y el almacenamiento de energía tiene costos que no son lineales. La PNL ayuda a encontrar la mezcla de energía más eficiente y con menor impacto ambiental.
Diseño de procesos químicos
En la industria química, la PNL se utiliza para mejorar los procesos. La relación entre la temperatura, la presión y la velocidad de las reacciones químicas suele ser no lineal. Los modelos de PNL ayudan a diseñar equipos, optimizar procesos y reducir el desperdicio, minimizando el consumo de energía o maximizando la producción.
Aprendizaje automático y redes neuronales
Entrenar redes neuronales es un problema de optimización no lineal. El objetivo es reducir al mínimo el error entre lo que la red predice y lo que realmente sucede. Los algoritmos de PNL se usan para ajustar los valores internos de la red de manera eficiente y lograr el mejor rendimiento.
Galería de imágenes
-
La intersección de la línea con el espacio de restricciones representa la solución.
-
La intersección de la superficie superior con el espacio de restricciones en el centro representa la solución.
Véase también
En inglés: Nonlinear programming Facts for Kids
