Problema de Monty Hall para niños
El problema de Monty Hall es un problema matemático de probabilidad que se basa en un famoso concurso televisivo de Estados Unidos llamado Trato hecho. Este desafío fue presentado por el matemático Steve Selvin en 1975 y se hizo muy popular gracias a Marilyn vos Savant en 1990. El problema lleva el nombre de Monty Hall, el presentador de aquel programa.
Contenido
¿Cómo funciona el juego?
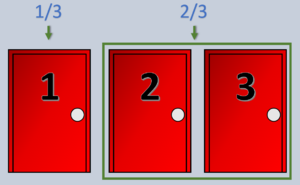
Imagina que estás en un concurso de televisión. Tienes que elegir una de tres puertas cerradas. Detrás de una de ellas hay un coche (¡el gran premio!), y detrás de las otras dos hay cabras.
1. Primero, eliges una puerta, por ejemplo, la Puerta 1. 2. El presentador, que sabe dónde está el coche, abre una de las otras dos puertas (la que no elegiste) y siempre muestra una cabra. ¡Nunca abrirá la puerta que elegiste ni la que tiene el coche! 3. Después de que el presentador muestra la cabra, te pregunta: "¿Quieres cambiar tu elección a la otra puerta que sigue cerrada, o prefieres quedarte con la que elegiste al principio?".
La pregunta clave es: ¿Es mejor cambiar de puerta o quedarte con la primera que elegiste? ¿Hay alguna diferencia en tus posibilidades de ganar?
Esta pregunta causó mucho debate porque la respuesta correcta parece ir en contra de lo que la mayoría de la gente piensa. Por eso se le llama una paradoja.
Las reglas del juego
Para entender bien el problema, hay que tener en cuenta estas reglas importantes sobre cómo actúa el presentador:
- El presentador siempre abre una puerta después de que tú eliges.
- La puerta que abre el presentador siempre tiene una cabra. Él sabe dónde está el coche y las cabras.
- El presentador elige qué puerta abrir de las dos que no elegiste, después de que tú hayas hecho tu primera elección.
La solución: ¿Debes cambiar de puerta?
La respuesta es: ¡Sí, es mejor cambiar de puerta! Si cambias, tienes más posibilidades de ganar el coche.
Entendiendo las probabilidades
Al principio, cuando eliges una puerta, tienes 1 posibilidad de 3 (o 1/3) de haber elegido la puerta con el coche. Esto significa que hay 2 posibilidades de 3 (o 2/3) de que el coche esté detrás de una de las otras dos puertas que no elegiste.
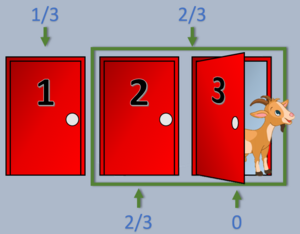
Cuando el presentador abre una puerta y muestra una cabra, ¡esto cambia las cosas! La puerta que se abrió ahora tiene 0% de probabilidad de tener el coche. Pero la probabilidad de 2/3 que tenían las otras dos puertas (el grupo que no elegiste) no desaparece. Esa probabilidad se concentra en la única puerta que queda cerrada de ese grupo.
- Si te quedas con tu elección original: Solo ganas si tu primera elección (con 1/3 de probabilidad) fue la correcta.
- Si cambias de puerta: Ganas si tu primera elección (con 2/3 de probabilidad) fue una cabra. En ese caso, el presentador te "ayuda" al eliminar la otra cabra, dejando la puerta del coche como la única opción restante.
En resumen, al cambiar de puerta, pasas de tener 1/3 de probabilidad de ganar a tener 2/3 de probabilidad de ganar. ¡Es el doble de posibilidades!
| Detrás de la puerta 1 | Detrás de la puerta 2 | Detrás de la puerta 3 | Resultado si te quedas con la puerta 1 | Resultado si cambias de puerta |
|---|---|---|---|---|
| Cabra | Cabra | Coche | Ganas una cabra | Ganas un coche |
| Cabra | Coche | Cabra | Ganas una cabra | Ganas un coche |
| Coche | Cabra | Cabra | Ganas un coche | Ganas una cabra |
¿Por qué la intuición nos engaña?
Mucha gente piensa que, una vez que quedan solo dos puertas cerradas, la probabilidad de que el coche esté en cualquiera de ellas es 1/2 (50%). Pero esto no es así, porque la acción del presentador no es al azar. Él sabe dónde está el coche y siempre abre una puerta con una cabra. Esta información es clave.
Imagina que eliges la Puerta 1.
- Si el coche está en la Puerta 1 (1/3 de probabilidad), el presentador puede abrir la Puerta 2 o la Puerta 3. Si cambias, pierdes.
- Si el coche está en la Puerta 2 (1/3 de probabilidad), el presentador *debe* abrir la Puerta 3. Si cambias a la Puerta 2, ganas.
- Si el coche está en la Puerta 3 (1/3 de probabilidad), el presentador *debe* abrir la Puerta 2. Si cambias a la Puerta 3, ganas.
Como puedes ver, en 2 de cada 3 casos (cuando el coche no está en tu primera elección), cambiar te asegura la victoria.
Un ejemplo con muchas puertas
Para entenderlo aún mejor, imagina que en lugar de 3 puertas, hay 100 puertas. Tú eliges una, digamos la Puerta 1. El presentador, que sabe dónde está el coche, abre 98 de las otras 99 puertas, ¡y todas tienen cabras! Solo quedan dos puertas cerradas: la que elegiste al principio y otra más.
¿Qué harías? ¿Te quedarías con tu Puerta 1 (que tenías 1/100 de probabilidad de que fuera la correcta) o cambiarías a la otra puerta que el presentador dejó cerrada?
En este caso, es mucho más claro que la probabilidad de que el coche estuviera en el grupo de las 99 puertas que no elegiste era de 99/100. Al abrir 98 cabras, esa probabilidad de 99/100 se concentra en la única puerta que queda cerrada de ese grupo. ¡Así que cambiar te daría un 99% de posibilidades de ganar!
Explicación con sobres y cajas
Piensa en tres sobres y dos cajas vacías: Caja 1 y Caja 2. Solo uno de los sobres tiene un premio.
1. Eliges un sobre y lo pones en la Caja 1. 2. Los otros dos sobres los pones en la Caja 2. 3. Ahora, el presentador te dice: "Voy a sacar un sobre sin premio de la Caja 2 y te lo voy a mostrar. Luego, ¿quieres cambiar tu Caja 1 por la Caja 2 (que ahora solo tiene un sobre dentro)?"
La Caja 1 (con tu sobre elegido) tenía 1/3 de probabilidad de tener el premio. La Caja 2 (con los otros dos sobres) tenía 2/3 de probabilidad de tener el premio. Cuando el presentador saca un sobre sin premio de la Caja 2, ¡no cambia el valor de la Caja 2! Sigue teniendo 2/3 de probabilidad de contener el premio. Por lo tanto, ¡deberías cambiar a la Caja 2!
En la cultura popular
El problema de Monty Hall ha aparecido en varias series y películas, mostrando cómo la lógica puede ser diferente de la intuición:
- En un episodio de la serie Los cazadores de mitos, investigaron este problema.
- En la serie Friends, el personaje Chandler Bing lo menciona.
- En el libro El curioso incidente del perro a medianoche, se usa para explicar cómo la lógica nos ayuda a veces más que la intuición.
- En la película 21 blackjack, un profesor de matemáticas desafía a sus alumnos con este problema.
- También aparece en la serie Brooklyn Nine-Nine y The Hollow.
- El capítulo 4 de la primera temporada de la serie D. P.: El cazadesertores se titula «El problema de Monty Hall» y lo usa para explicar las decisiones de un personaje.
Véase también
 En inglés: Monty Hall problem Facts for Kids
En inglés: Monty Hall problem Facts for Kids