Principio del palomar para niños
El principio del palomar, también conocido como principio de las casillas o principio de Dirichlet, es una idea sencilla pero muy útil en Matemática. Dice que si tienes más objetos que lugares para guardarlos, entonces al menos un lugar tendrá más de un objeto.
Imagina que tienes 7 palomas y 6 palomares. Si cada paloma entra en un palomar diferente, solo podrías acomodar 6 palomas. Pero como tienes 7, la séptima paloma tendrá que ir a un palomar que ya tiene una paloma. ¡Así, al menos un palomar tendrá dos o más palomas!
Aunque parece muy obvio, este principio se usa para resolver problemas que a primera vista parecen complicados.
Este principio fue mencionado por primera vez en un libro de 1624 atribuido a Jean Leurechon. Sin embargo, se le conoce más como el "Principio de las cajas de Dirichlet" porque el matemático Johann Peter Gustav Lejeune Dirichlet lo explicó en un tratado en 1834. Él lo llamó Schubfachprinzip, que significa "principio de los cajones".
Contenido
¿De dónde viene el nombre?
Dirichlet usó la palabra alemana Schubfach o la francesa tiroir, que significan "cajón". Él hablaba de guardar perlas en esos cajones. Con el tiempo, la idea de "cajón" o "casilla" se relacionó con los "palomares", que son pequeños espacios donde las palomas viven o donde se guardan cartas y papeles.
Por eso, aunque originalmente se refería a cajones, ahora lo conocemos como el "principio del palomar". Incluso en alemán, a veces se le llama "Taubenschlagprinzip", que significa "principio del palomar", como una traducción de vuelta.
¿Cómo se explica de forma más general?
El principio del palomar se puede usar de varias maneras. Una forma más general dice que si tienes 
objetos y los distribuyes en 
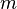grupos, entonces al menos uno de los grupos tendrá un número de objetos igual o mayor que dividido por 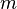, redondeado hacia arriba.
Por ejemplo, si tienes 10 objetos y 3 grupos, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10/3 es aproximadamente 3.33. Redondeado hacia arriba, es 4. Esto significa que al menos un grupo tendrá 4 o más objetos.
Este principio se usa mucho con grupos de cosas que se pueden contar, como personas o calcetines. También se usa en matemáticas más avanzadas para entender cómo funcionan los conjuntos infinitos.
Ejemplos divertidos del principio
El problema de los cumpleaños
Imagina que estás en una habitación con varias personas. ¿Cuántas personas necesitas para estar seguro de que al menos dos de ellas cumplen años el mismo día?
Si solo hay 366 días posibles en un año (incluyendo el 29 de febrero), entonces si hay 367 personas en la habitación, ¡es 100% seguro que al menos dos de ellas comparten el mismo día de cumpleaños! Esto es porque tienes más personas (objetos) que días posibles (lugares).
Sacando calcetines
Piensa que tienes una gaveta con calcetines azules y blancos, todos mezclados. No puedes ver los colores. ¿Cuántos calcetines necesitas sacar para estar seguro de que tienes un par del mismo color?
Aquí, los "lugares" son los colores (azul y blanco), así que hay 2 "lugares". Si sacas 3 calcetines (objetos), por el principio del palomar, al menos dos de ellos deben ser del mismo color. Podrías sacar dos azules y uno blanco, o dos blancos y uno azul, o incluso tres de un solo color. En cualquier caso, ¡tendrás un par!
Contando cabellos
Este es un ejemplo sorprendente: Hay al menos 2 personas en Guatemala con el mismo número de pelos en la cabeza.
¿Cómo sabemos esto? La cabeza de una persona tiene alrededor de 150,000 cabellos. Nadie tiene un millón de pelos. Podemos crear "lugares" para cada número de cabellos, desde 0 hasta 1,000,000. Cada persona es un "objeto" que va al "lugar" que corresponde a la cantidad de pelos que tiene. Como en Guatemala hay más de un millón de personas, ¡debe haber al menos dos personas con la misma cantidad de pelos!
¿Para qué se usa este principio?
El principio del palomar es muy útil en la informática. Por ejemplo, cuando las computadoras organizan información en algo llamado "tabla hash", a veces dos datos diferentes quieren ir al mismo lugar. Esto se llama "colisión" y es inevitable, porque hay más datos posibles que lugares en la tabla. El principio del palomar nos dice que estas colisiones siempre ocurrirán.
También nos ayuda a entender la compresión de archivos. Si un programa puede hacer que un archivo sea más pequeño sin perder información, entonces ese mismo programa hará que otro archivo sea más grande. Si no fuera así, dos archivos diferentes podrían comprimirse al mismo archivo pequeño, y luego no se sabría cuál era el original al descomprimirlo.
Galería de imágenes
-
La inspiración para el nombre del principio: aves en un palomar. Aquí
y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): m = 9 . -
Casillas de mensajes en Universidad Stanford.
-
Aquí Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n=10 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): m = 9 .
-
Si sacas dos calcetines la probabilidad de que sean iguales es del 1÷3
Ver también
- Combinatoria
- Principios combinatorios
- Teoría de Ramsey
Véase también
En inglés: Pigeonhole principle Facts for Kids
