Principio de mínima acción para niños
El principio de mínima acción es una idea fundamental en la física que nos ayuda a entender cómo se mueven las cosas en el universo. Imagina que la naturaleza siempre busca el camino más "eficiente" o "especial" para que las cosas se muevan. Este principio se usa para describir el movimiento de partículas muy pequeñas, como los electrones, y también de campos físicos, que son como energías que se extienden por el espacio.
Contenido
¿Qué es el Principio de Mínima Acción?
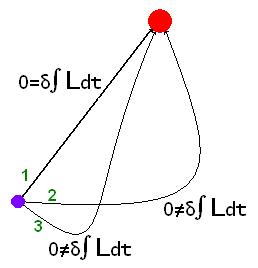
Este principio dice que, cuando un sistema físico se mueve de un punto a otro, no elige cualquier camino. En cambio, selecciona una trayectoria donde una cantidad llamada "acción" es lo más pequeña posible, o al menos, un valor "estacionario". Un valor estacionario es como la cima de una montaña o el fondo de un valle: un punto especial donde la "acción" no cambia mucho si te desvías un poquito.
¿Cómo se descubrió este principio?
La primera vez que se habló de esta idea fue en 1744, gracias a un científico llamado Pierre Louis Maupertuis. Él pensó que la naturaleza siempre es "económica" en sus movimientos. Otros científicos importantes como Leonhard Euler y Gottfried Leibniz también ayudaron a desarrollar esta idea.
Mucho antes, un matemático llamado Pierre de Fermat ya había notado algo parecido con la luz. Descubrió que los rayos de luz, al reflejarse o refractarse, siempre eligen el camino que les toma el menor tiempo posible. Esto es muy similar al principio de mínima acción.
Este principio fue muy importante porque llevó a nuevas formas de describir el movimiento, como las mecánicas lagrangiana y hamiltoniana. Estas formas son muy útiles para entender la Teoría de la Relatividad de Einstein y la mecánica cuántica, que estudian el mundo a escalas muy grandes y muy pequeñas.
¿Cómo se calcula la acción?
Para entender la acción, piensa en un viaje. La "acción" es como una suma de lo que ocurre en cada momento del viaje. El sistema elige el camino donde esta suma total es un valor especial.
Las ecuaciones de Euler-Lagrange
Para encontrar el camino "especial" que sigue un sistema, los científicos usan unas ecuaciones llamadas ecuaciones de Euler-Lagrange. Estas ecuaciones son como un mapa que les dice cuál es la trayectoria correcta para que la "acción" sea mínima o estacionaria.
La acción en campos físicos
El principio de mínima acción no solo funciona para partículas, sino también para campos físicos. Un campo físico es algo que se extiende por el espacio y el tiempo, como el campo eléctrico o el campo gravitatorio. Para estos campos, la acción se calcula de una manera un poco más compleja, sumando lo que ocurre en cada punto del espacio y en cada momento.
Principio de Mínima Acción y las Leyes de Newton
Es interesante saber que las famosas Leyes de Newton (las que explican cómo se mueven los objetos en nuestra vida diaria) pueden deducirse a partir del principio de mínima acción. Esto significa que ambas ideas están muy relacionadas y describen el mismo comportamiento de la naturaleza.
Por ejemplo, la primera ley de Newton dice que un objeto en movimiento seguirá moviéndose a velocidad constante si no hay fuerzas que lo detengan o lo empujen. Esta ley se puede entender usando el principio de mínima acción, asumiendo que el espacio es uniforme y no tiene direcciones preferidas.
El Principio de Mínima Acción en la Relatividad
En la Teoría de la Relatividad, que estudia el movimiento a velocidades muy altas o en campos gravitatorios muy fuertes, el principio de mínima acción sigue siendo muy útil.
Partículas en la Relatividad
En la relatividad, una partícula se mueve a lo largo de un camino especial en el espacio-tiempo llamado "geodésica". Piensa en una geodésica como la línea más "recta" posible en un espacio que puede estar curvado, como la superficie de una pelota. El principio de mínima acción nos ayuda a encontrar estas geodésicas.
Campos en la Relatividad
Los campos físicos, como el Campo electromagnético (que explica la luz y la electricidad) y el Campo gravitatorio (que explica la gravedad), también se describen con el principio de mínima acción en la relatividad.
Por ejemplo, las famosas ecuaciones de Maxwell, que describen cómo funcionan la electricidad y el magnetismo, se pueden obtener usando este principio. Lo mismo ocurre con las ecuaciones de campo de Einstein, que explican cómo la gravedad curva el espacio-tiempo.
El Principio de Mínima Acción y la Mecánica Cuántica
Incluso en la mecánica cuántica, que estudia el mundo a escalas increíblemente pequeñas (átomos y partículas subatómicas), el principio de mínima acción ha inspirado nuevas formas de entender cómo se comportan las partículas. Aunque es un poco diferente, la idea de que las partículas eligen un camino "especial" sigue siendo muy importante.
Véase también
- Cálculo de variaciones
- Acción