Método de Newton para niños
El método de Newton es una herramienta matemática muy útil que nos ayuda a encontrar los "ceros" o "raíces" de una función. Imagina que tienes el dibujo de una función en una gráfica; los ceros son los puntos donde la línea de la función cruza el eje horizontal (el eje X). Este método también se conoce como el método de Newton-Raphson y es un tipo de algoritmo, que es como una serie de pasos o instrucciones para resolver un problema.
Además de encontrar los ceros, el método de Newton puede usarse para hallar el punto más alto o más bajo de una función. Para hacer esto, se buscan los ceros de otra función especial llamada su "derivada", que nos dice cómo cambia la función original.
Contenido
Historia del Método de Newton
El famoso científico Isaac Newton fue quien describió este método en sus escritos. Lo hizo en un libro llamado De analysi per aequationes numero terminorum infinitas (escrito en 1669, pero publicado en 1711) y en otro llamado De metodis fluxionum et serierum infinitarum (escrito en 1671, publicado en 1736).
Sin embargo, la forma en que Newton lo describió era un poco diferente a cómo lo usamos hoy. Él lo aplicaba solo a polinomios (expresiones matemáticas con sumas y restas de términos con potencias de una variable) y no usaba las aproximaciones paso a paso como se hace ahora. Newton veía su método como algo puramente algebraico y no se dio cuenta de su conexión con el cálculo, una rama de las matemáticas que estudia el cambio.
Se cree que Isaac Newton se inspiró en trabajos anteriores, como los del matemático persa Sharaf al-Din al-Tusi y el francés François Viète.
El nombre "Newton-Raphson" se debe a Joseph Raphson, un matemático inglés que vivió en la misma época que Newton. Raphson publicó un libro en 1690 llamado Aequationum Universalis, donde describía este método para encontrar raíces. Aunque Newton había descrito el mismo método antes, su trabajo no se publicó hasta mucho después, por lo que Raphson fue el primero en publicarlo.
¿Cómo Funciona el Método de Newton?
El método de Newton es como un juego de adivinanzas, pero con reglas matemáticas. Para empezar, necesitas hacer una primera suposición de dónde crees que está el cero de la función. A esta suposición la llamamos x0.
Luego, el método funciona así:
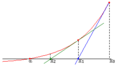
- En el punto de tu suposición (x0), trazas una línea recta que toca la curva de la función en ese único punto. Esta línea se llama "tangente".
- Observas dónde esta línea tangente cruza el eje X. Ese punto es tu nueva y mejor suposición para el cero de la función. A este nuevo punto lo llamamos x1.
- Repites el proceso: desde x1, trazas otra línea tangente a la función y encuentras dónde cruza el eje X. Ese será tu x2, y así sucesivamente.
Cada vez que repites este paso, tu nueva suposición se acerca más y más al verdadero cero de la función. El proceso se detiene cuando la suposición es lo suficientemente precisa.
La fórmula que se usa para calcular la siguiente suposición es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}} Donde:
- xn+1 es tu nueva y mejor suposición.
- xn es tu suposición actual.
- f(xn) es el valor de la función en tu suposición actual.
- f'(xn) es el valor de la derivada de la función en tu suposición actual. La derivada nos dice la inclinación de la línea tangente en ese punto.
Es muy importante que tu primera suposición (x0) esté lo suficientemente cerca del cero real. Si está muy lejos, el método podría no funcionar y tus suposiciones podrían alejarse del cero en lugar de acercarse.
¿De Dónde Viene la Fórmula?
La fórmula del método de Newton se puede entender de varias maneras. La más sencilla es la interpretación geométrica que ya explicamos:
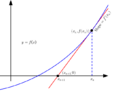
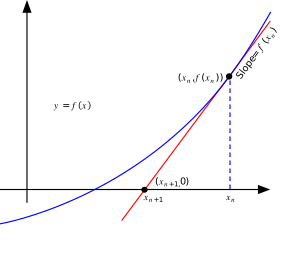
Imagina que tienes un punto (xn, f(xn)) en la gráfica de la función. La pendiente de la línea tangente en ese punto es igual a la derivada de la función, f'(xn).
Sabemos que la pendiente de una línea se calcula como el cambio vertical dividido por el cambio horizontal. En este caso, el cambio vertical es f(xn) - 0 (porque la tangente cruza el eje X en xn+1), y el cambio horizontal es xn - xn+1.
Así, podemos escribir: 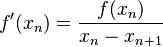
Si reorganizamos esta ecuación para despejar xn+1, obtenemos la fórmula del método de Newton: 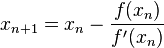
Como puedes ver en las ilustraciones, cada nueva suposición xn+1 está más cerca del cero de la función que la suposición anterior xn.
¿Qué Tan Rápido Encuentra la Respuesta?
El método de Newton es muy eficiente. Se dice que tiene una "convergencia cuadrática". Esto significa que, si tu suposición ya es bastante buena, el número de dígitos correctos en tu respuesta se duplica aproximadamente con cada paso que das. Por ejemplo, si en un paso tienes 2 dígitos correctos, en el siguiente podrías tener 4, y en el siguiente 8, y así sucesivamente. ¡Es muy rápido!
Sin embargo, hay algunas situaciones en las que el método puede ser más lento o incluso no funcionar:
- Si la función tiene un cero "múltiple" (como si la curva solo toca el eje X y rebota, en lugar de cruzarlo), el método es más lento.
- Si tu primera suposición está muy lejos del cero, el método podría no encontrarlo o incluso irse en la dirección equivocada. Por eso, es importante empezar con una suposición razonable.
Ejemplo Práctico
Vamos a usar el método de Newton para encontrar un número positivo x tal que 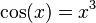 . Para usar el método, necesitamos una función que sea igual a cero en la solución. Así que, podemos reescribir la ecuación como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x)=\cos(x)-x^3=0 .
. Para usar el método, necesitamos una función que sea igual a cero en la solución. Así que, podemos reescribir la ecuación como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x)=\cos(x)-x^3=0 .
También necesitamos la derivada de esta función, que es 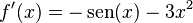 .
.
Sabemos que la solución debe estar entre 0 y 1. Vamos a empezar con una suposición inicial de  .
.
Ahora, aplicamos la fórmula paso a paso:
- Paso 1:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} = 0,5 - \frac{\cos(0,5) - 0,5^3}{-\sin(0,5) - 3 \times 0,5^2} \approx 1,112141637097
- Paso 2:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} \approx 0,909672693736
- Paso 3:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_3 = x_2 - \frac{f(x_2)}{f'(x_2)} \approx 0,867263818209
- Paso 4:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_4 = x_3 - \frac{f(x_3)}{f'(x_3)} \approx 0,865477135298
- Paso 5:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_5 = x_4 - \frac{f(x_4)}{f'(x_4)} \approx 0,865474033111
- Paso 6:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_6 = x_5 - \frac{f(x_5)}{f'(x_5)} \approx 0,865474033102
Como puedes ver, en cada paso, el número de dígitos correctos (subrayados) aumenta rápidamente. En el paso 6, ya tenemos una respuesta muy precisa. Esto demuestra lo rápido que el método de Newton puede encontrar una solución.
Galería de imágenes
-
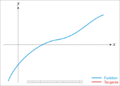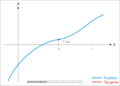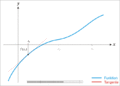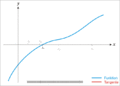
Ilustración de algunas líneas generadas por el método de Newton–Raphson fraccional para la misma condición inicial
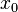 pero con diferentes órdenes
pero con diferentes órdenes  del operador fraccional implementado. El método de Newton–Raphson fraccional generalmente genera líneas que no son tangentes a la función
del operador fraccional implementado. El método de Newton–Raphson fraccional generalmente genera líneas que no son tangentes a la función  cuyas raíces se buscan, a diferencia del método clásico de Newton–Raphson.
cuyas raíces se buscan, a diferencia del método clásico de Newton–Raphson.
Véase también
 En inglés: Newton's method Facts for Kids
En inglés: Newton's method Facts for Kids


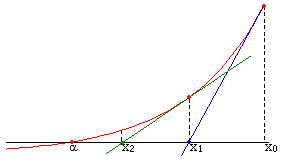
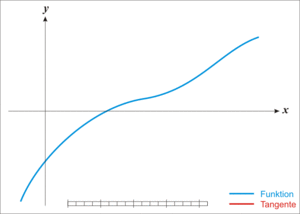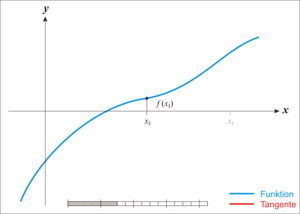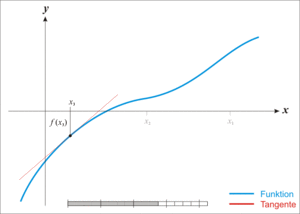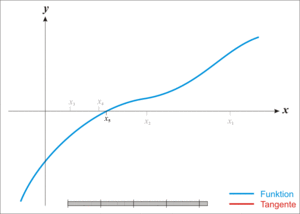
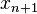 es una aproximación mejor que
es una aproximación mejor que 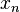 para la raíz
para la raíz  de la función
de la función