Máximo común divisor para niños

En las matemáticas, el máximo común divisor (conocido como MCD o m.c.d.) de dos o más números enteros es el número entero más grande que puede dividir a esos números sin dejar ningún residuo. Es como encontrar el "factor común" más grande que tienen varios números.

¿Qué es el Máximo Común Divisor?

Imagina que tienes dos números, por ejemplo, 12 y 18. Los divisores de 12 son 1, 2, 3, 4, 6 y 12. Los divisores de 18 son 1, 2, 3, 6, 9 y 18.

Los divisores que tienen en común 12 y 18 son 1, 2, 3 y 6. De todos esos divisores comunes, el más grande es 6. Por lo tanto, el máximo común divisor de 12 y 18 es 6.

Un número d es el máximo común divisor de otros números a y b si cumple dos cosas:

• d es un divisor de a y también de b.
• d es el divisor común más grande que existe entre a y b.

Ejemplo: El MCD de 36 y 60 es 12. Esto es porque 12 divide a 36 (36 ÷ 12 = 3) y 12 divide a 60 (60 ÷ 12 = 5). Además, 12 es el número más grande que puede dividir a ambos sin dejar residuo.

Cómo calcular el Máximo Común Divisor

Existen varios métodos para encontrar el MCD de dos o más números. Aquí te explicamos los más comunes:

Usando la descomposición en factores primos

Este método consiste en descomponer cada número en sus factores primos. Luego, multiplicas los factores primos que tienen en común, pero usando el exponente más pequeño de cada uno.

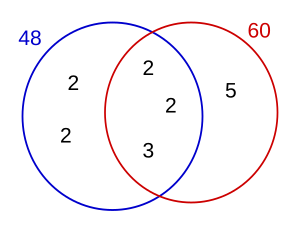
Ejemplo: Calcular el MCD de 48 y 60.

Primero, descomponemos 48 y 60 en sus factores primos:

Descomposición en factores primos de 48 y 60.

• 48 = 2 × 2 × 2 × 2 × 3 = 2⁴ × 3
• 60 = 2 × 2 × 3 × 5 = 2² × 3 × 5

Ahora, identificamos los factores primos que tienen en común: el 2 y el 3.

• Para el factor 2, el exponente más pequeño es 2² (de 60).
• Para el factor 3, el exponente más pequeño es 3¹ (está en ambos).
• El factor 5 no es común, así que no lo usamos.

Multiplicamos los factores comunes con sus exponentes más pequeños: MCD (48, 60) = 2² × 3 = 4 × 3 = 12

Este método es útil para números pequeños. Para números muy grandes, puede ser complicado encontrar todos sus factores primos.

Usando el algoritmo de Euclides

El algoritmo de Euclides es un método muy eficiente para encontrar el MCD, especialmente para números grandes. Se basa en una regla sencilla: el MCD de dos números también divide al resto que se obtiene al dividir el número más grande entre el más pequeño.

Ejemplo 1: Calcular el MCD de 60 y 48.

1. Divide 60 entre 48: 60 ÷ 48 = 1 con un resto de 12.
2. Ahora, el MCD de 60 y 48 es el mismo que el MCD de 48 y el resto (12).
3. Divide 48 entre 12: 48 ÷ 12 = 4 con un resto de 0.
4. Cuando el resto es 0, el último divisor que usaste (en este caso, 12) es el MCD.

Así, el MCD (60, 48) = 12.

Ejemplo 2: Calcular el MCD de 42 y 56.

1. Divide 56 entre 42: 56 ÷ 42 = 1 con un resto de 14.
2. Ahora, el MCD de 56 y 42 es el mismo que el MCD de 42 y el resto (14).
3. Divide 42 entre 14: 42 ÷ 14 = 3 con un resto de 0.
4. El último divisor fue 14, así que el MCD (42, 56) = 14.

Usando el mínimo común múltiplo

También puedes calcular el MCD si ya conoces el mínimo común múltiplo (mcm) de los números. La fórmula es la siguiente: MCD (a, b) = (a × b) / mcm (a, b)

Por ejemplo, si el mcm de 48 y 60 es 240, entonces: MCD (48, 60) = (48 × 60) / 240 = 2880 / 240 = 12

MCD de tres o más números

Para encontrar el MCD de tres o más números, puedes hacerlo paso a paso. Primero, calculas el MCD de los dos primeros números. Luego, calculas el MCD de ese resultado y el tercer número, y así sucesivamente.

Por ejemplo, para encontrar el MCD de a, b y c: MCD (a, b, c) = MCD (a, MCD (b, c))

Propiedades importantes del MCD

• Si divides dos números por su MCD, los resultados serán primos entre sí (su MCD será 1). Por ejemplo, MCD(48, 60) = 12. Si divides 48/12 = 4 y 60/12 = 5. El MCD(4, 5) = 1.
• Si multiplicas dos números por un mismo valor, su MCD también se multiplicará por ese valor.
• Si un número primo p divide a otro número m, entonces el MCD de p y m será p. Si p no divide a m, entonces su MCD será 1.
• El MCD de dos números es el producto de sus factores primos comunes, cada uno elevado al exponente más pequeño que tenga en las descomposiciones.

Aplicaciones del Máximo Común Divisor

El MCD es muy útil en matemáticas y en la vida diaria:

• Simplificar fracciones: Para simplificar una fracción, divides tanto el numerador como el denominador por su MCD. Por ejemplo, para simplificar la fracción 48/60, calculamos que el MCD(48, 60) es 12. Dividimos 48 ÷ 12 = 4 y 60 ÷ 12 = 5. Así, la fracción simplificada es 4/5.
• Calcular el mínimo común múltiplo: Como vimos antes, el MCD y el mcm están relacionados. Si conoces el MCD de dos números, puedes calcular su mcm.
• Resolver problemas: El MCD se usa para resolver problemas donde necesitas dividir algo en partes iguales lo más grandes posible, o para agrupar elementos de la manera más eficiente.

Véase también

En inglés: Greatest common divisor Facts for Kids

• Mínimo común múltiplo
• Números primos entre sí