Momento magnético para niños
El momento magnético es una medida que nos dice qué tan fuerte es una fuente de campo magnético y hacia dónde apunta su magnetismo. Piensa en ello como la "personalidad magnética" de un objeto. Esta fuente puede ser un imán común, una corriente eléctrica que gira en un círculo, un electrón, una molécula o incluso un planeta.
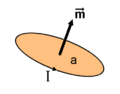
Tanto el momento magnético como el campo magnético son como flechas (vectores) que tienen una fuerza (magnitud) y una dirección. La dirección del momento magnético va desde el polo sur hacia el polo norte de un imán. El campo magnético que produce un imán es más fuerte cuanto mayor es su momento magnético. Si hablamos de una corriente eléctrica que forma un círculo, su momento magnético apunta perpendicularmente al área que encierra, siguiendo la regla de la mano derecha.
Cuando un objeto con momento magnético se encuentra en un campo magnético externo, experimenta una fuerza que intenta alinearlo con ese campo. Cuanto mayor sea el momento magnético del objeto, mayor será esta fuerza de alineación. La fuerza y la dirección de esta fuerza no solo dependen de la intensidad del momento magnético, sino también de cómo está orientado respecto al campo magnético externo.
Contenido
- Momento Magnético: ¿Qué es y por qué es importante?
- Galería de imágenes
- Véase también
Momento Magnético: ¿Qué es y por qué es importante?
El momento magnético es una propiedad fundamental en la física que nos ayuda a entender cómo interactúan los objetos con los campos magnéticos. Es crucial para explicar desde el funcionamiento de una brújula hasta el comportamiento de las partículas más pequeñas.
¿Cómo se define el momento magnético?
El momento magnético se puede definir como un vector que nos muestra cómo un campo magnético externo ejerce una fuerza de giro (llamada par) sobre un objeto. La relación se describe con la siguiente fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle \boldsymbol{\tau} = \mathbf{m} \times\mathbf{B}}
Donde:
- τ es el par (la fuerza de giro) que actúa sobre el objeto.
- B es el campo magnético externo.
- m es el momento magnético del objeto.
Esta definición nos permite, por ejemplo, calcular el momento magnético de un circuito por el que pasa una corriente. Para un bucle de corriente, la fuerza de su momento magnético es igual al producto de la corriente que circula por el área del bucle.
Unidades de medida del momento magnético
En el Sistema Internacional de Unidades (SI), la unidad para el momento magnético es el amperio por metro cuadrado (A·m²). Esta unidad también se puede expresar como joule por tesla (J/T).
Para medir los momentos magnéticos de partículas muy pequeñas, como los electrones o los núcleos de los átomos, se usan unidades especiales llamadas magnetón de Bohr y magnetón nuclear.
¿Cómo se mide el momento magnético?
Los momentos magnéticos de los objetos se miden con aparatos especiales llamados magnetómetros. Algunos magnetómetros miden directamente el campo magnético, y a partir de esa información, se puede calcular el momento magnético del objeto.
Momento magnético y magnetización
El momento magnético describe la fuerza magnética de un objeto completo. Sin embargo, a veces es útil saber cuánto de ese magnetismo total es producido por una parte específica del objeto. Para esto, usamos el concepto de magnetización.
¿Qué es la magnetización?
La magnetización (representada como M) es el momento magnético por unidad de volumen. Es decir, nos dice cuánto magnetismo hay "empaquetado" en un cierto espacio dentro de un material. Se calcula dividiendo el momento magnético de una pequeña porción del material entre el volumen de esa porción.
Si la magnetización es uniforme en todo el objeto (es decir, la fuerza y dirección de M son las mismas en todas partes), entonces el momento magnético total del objeto es simplemente la magnetización multiplicada por su volumen.
¿Cómo se relaciona con otras fuerzas?
El momento magnético se relaciona con el par de fuerzas que experimenta un objeto en un campo magnético. La fórmula es:
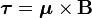
Donde 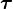 es el par de fuerzas,
es el par de fuerzas, 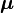 es el momento magnético, y
es el momento magnético, y 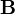 es el campo magnético.
es el campo magnético.
Además, la alineación del momento magnético con el campo magnético cambia la energía potencial del sistema:
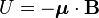
Un ejemplo sencillo es el de una espira (un bucle) por la que circula una corriente eléctrica. Si la corriente es I y el área de la espira es A, la magnitud de su momento magnético es:
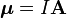
El momento magnético de las partículas pequeñas
Los electrones y muchos núcleos atómicos tienen sus propios momentos magnéticos, que son una propiedad fundamental de ellos. Estos momentos magnéticos intrínsecos son los que causan los efectos magnéticos que vemos a gran escala, como los imanes que usamos todos los días.
Momento magnético de espín
El momento magnético de espín es una propiedad "interna" de las partículas, como su masa o su carga eléctrica. Está relacionado con el hecho de que las partículas elementales tienen un "giro" o espín propio. Para las partículas con carga, este giro hace que se comporten como pequeños circuitos con cargas en movimiento, generando un momento magnético. Curiosamente, incluso partículas sin carga eléctrica, como el neutrón, tienen momento magnético porque están formadas por partículas más pequeñas (los quarks) que sí tienen carga.
| Partícula | Símbolo | Valor (J/T) | Valor (magnetones) |
|---|---|---|---|
| Protón | 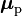 |
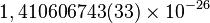 |
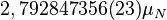 |
| Neutrón | 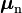 |
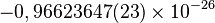 |
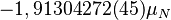 |
| Electrón | 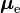 |
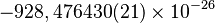 |
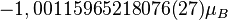 |
| Muon | 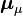 |
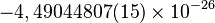 |
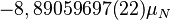 |
Momento magnético orbital
Además del espín, los electrones en los átomos también pueden tener un momento magnético debido a su movimiento alrededor del núcleo, similar a cómo una corriente en un bucle crea un campo magnético. Esto se llama momento magnético orbital. Es como si cada electrón fuera un pequeño imán girando en su órbita.
Modelos para entender el momento magnético
A lo largo del tiempo, los científicos han usado diferentes modelos para explicar el momento magnético.
El modelo de polo magnético
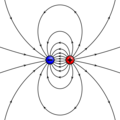
Un modelo clásico para entender los momentos magnéticos es el de los polos magnéticos. En este modelo, un imán pequeño se imagina como si tuviera dos "polos" magnéticos imaginarios: uno norte y uno sur, con la misma fuerza pero opuestos. Cada polo es una fuente de fuerza magnética que se debilita con la distancia. Como los polos magnéticos siempre vienen en pares, sus fuerzas se anulan parcialmente. Esta anulación es mayor cuando los polos están muy cerca.
La fuerza magnética que produce un imán en un punto dado depende de la fuerza de sus polos y de la distancia que los separa. El momento magnético se relaciona con estos polos imaginarios y apunta desde el polo sur hacia el polo norte. Aunque este modelo es útil para algunos cálculos, es importante recordar que los polos magnéticos no existen de forma separada, a diferencia de las cargas eléctricas.
Galería de imágenes
Véase también
 En inglés: Magnetic moment Facts for Kids
En inglés: Magnetic moment Facts for Kids


 de algunas
de algunas