Moda (estadística) para niños

En estadística, la moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Imagina que tienes una lista de los colores favoritos de tus amigos. Si el "azul" es el color que más amigos eligieron, entonces el "azul" es la moda de esa lista.

A veces, un conjunto de datos puede tener dos valores que aparecen con la misma frecuencia máxima. A esto se le llama una distribución bimodal. Si hay tres valores con la misma frecuencia máxima, se llama trimodal. Si todos los datos tienen la misma frecuencia, algunos matemáticos dicen que no hay moda, porque ningún valor se destaca.

El intervalo modal es el grupo de datos que tiene la mayor frecuencia. Cuando los datos están agrupados en intervalos, primero se identifica este intervalo modal para luego encontrar la moda.

La moda también se usa en el mundo de las finanzas, por ejemplo, para identificar el precio más común de un producto en un período de tiempo.

Historia de la Moda en Matemáticas

El término "moda" en estadística fue usado por primera vez en 1895 por Karl Pearson. Se inspiró en la idea de "estar a la moda", que se refiere a algo que es muy popular o usado por muchas personas, como un tipo de coche o un teléfono móvil. Así, si en la vida diaria "moda" significa "muy usado", en estadística significa el valor más frecuente en un grupo de datos.

Hay una historia antigua que se relaciona con este concepto. Durante un asedio en la antigua Grecia, los soldados necesitaban construir escaleras para escapar. Para saber qué tan altas debían ser las escaleras, muchos contaron las capas de ladrillos de las murallas enemigas. Aunque algunos pudieron haber cometido errores, la mayoría de los recuentos habrían sido correctos. Esto significa que el número que más se repitió en sus conteos era el más confiable, ¡como una moda!

Moda de una Muestra

Ilustración del cálculo de la moda de una población. Para la población {1, 7, 4, 6, 5, 5, 3, 5}, la moda es 5.

Ilustración del comportamiento de las medidas de tendencia central en una distribución simétrica (por ejemplo, una distribución normal) cuando cambia la dispersión de los datos. La curva roja describe la densidad de probabilidad en el espacio muestral y la línea azul representa la ubicación de la media, la mediana y la moda del conjunto de datos.

Ilustración del comportamiento de las medidas de tendencia central en una distribución asimétrica negativa cuando se altera la dispersión de los datos. La curva roja describe la densidad de probabilidad en el espacio muestral, la línea azul (a la izquierda) representa la media, la línea amarilla (en el centro) representa la mediana y la línea verde (a la derecha) representa la moda del conjunto de datos.

Ilustración del comportamiento de las medidas de tendencia central en una distribución asimétrica positiva (por ejemplo, una distribución chi-cuadrado) cuando se altera la dispersión de los datos. La curva roja describe la densidad de probabilidad de los datos en el espacio muestral, la línea azul (derecha) representa la media, la línea amarilla (centro) representa la mediana y la línea verde (izquierda) representa la moda del conjunto de datos.

Ilustración del comportamiento de las medidas de tendencia central en una distribución bimodal, formada por otras dos distribuciones con sus respectivos parámetros, que transita entre la distribución asimétrica positiva, la distribución asimétrica negativa y la distribución simétrica a medida que se alteran las dispersiones de los datos en el espacio muestral. La curva roja describe la densidad de probabilidad de los datos en el espacio muestral, la línea azul representa la media, la línea amarilla representa la mediana y la línea verde representa la moda del conjunto de datos

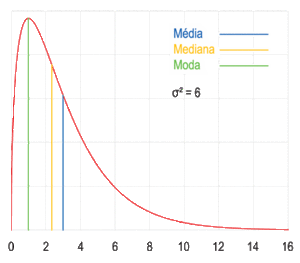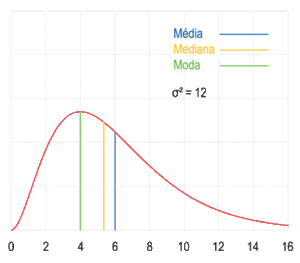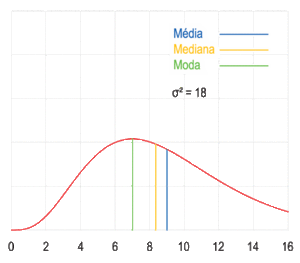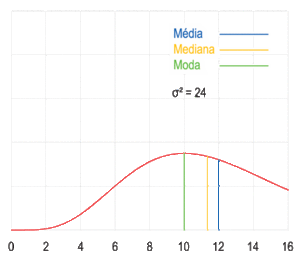
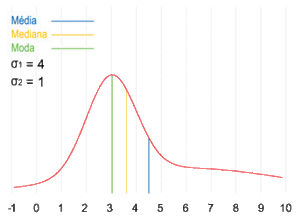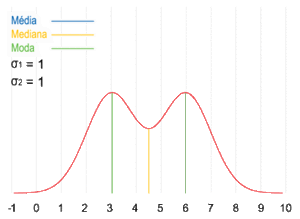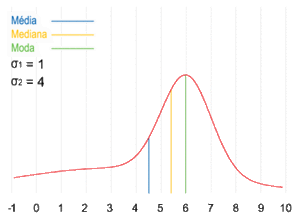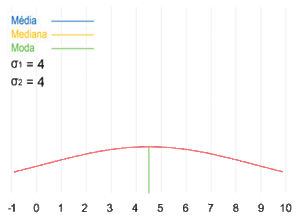
Una muestra de datos puede ser:

• Unimodal: Tiene una sola moda.
• Bimodal: Tiene dos modas.
• Multimodal: Tiene varias modas.
• Amodal: No tiene moda (todos los valores aparecen con la misma frecuencia).

Por ejemplo, en la lista de números [1, 3, 6, 6, 6, 6, 7, 7, 12, 12, 17], la moda es 6, porque aparece cuatro veces, más que cualquier otro número. En la lista [1, 1, 2, 4, 4], tanto el 1 como el 4 aparecen dos veces, así que es bimodal.

¿Para qué sirve la Moda?

A diferencia de la media (el promedio) y la mediana (el valor central), la moda es muy útil para datos que no son números. Por ejemplo, si preguntas a un grupo de personas cuál es su fruta favorita, y la mayoría dice "manzana", entonces "manzana" es la moda. No podrías calcular un promedio o una mediana con nombres de frutas.

En un sistema de votación, si un candidato obtiene la mayor cantidad de votos, ese es el ganador, y su resultado sería la moda. Si hay un empate entre varios candidatos, se necesitaría un desempate.

Unicidad y Definición

La moda no siempre es única. Un conjunto de datos puede tener una, dos o más modas. En cambio, la media de un conjunto de datos siempre es única. La mediana, que es el valor central cuando los datos están ordenados, puede no ser única en algunos casos, pero siempre está definida.

Propiedades de la Moda

• Si cambias todos los valores de un conjunto de datos de la misma manera (por ejemplo, multiplicándolos por un número y luego sumando otro), la moda también cambiará de la misma manera.
• La moda no se ve afectada por valores muy diferentes al resto (llamados valores atípicos o outliers). Por ejemplo, si en una lista de edades de 12, 13, 14, 13, 12, 100, la moda sigue siendo 12 y 13, a pesar del 100. La media, en cambio, sí se vería muy afectada por el 100.

Moda de Datos Agrupados

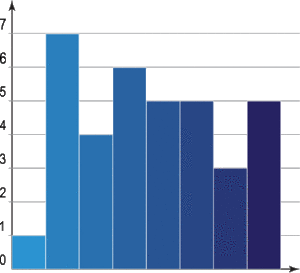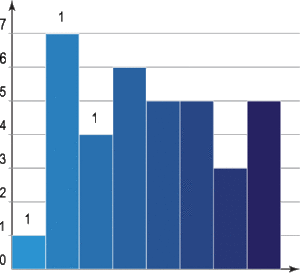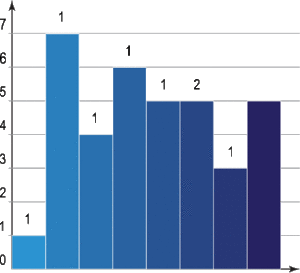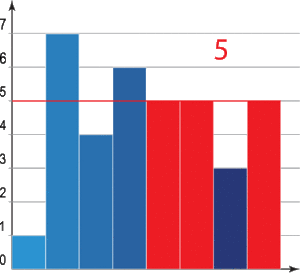
Cuando los datos están agrupados en intervalos (como en un histograma), se usa una fórmula especial para calcular la moda. Esta fórmula ayuda a encontrar el punto exacto dentro del intervalo con mayor frecuencia.

La fórmula para la moda en datos agrupados es: 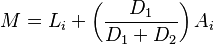Donde:

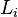• es el límite inferior del intervalo que tiene la mayor frecuencia (el intervalo modal).
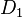• es la diferencia entre la frecuencia del intervalo modal y la frecuencia del intervalo anterior.
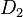• es la diferencia entre la frecuencia del intervalo modal y la frecuencia del intervalo siguiente.
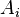• es la amplitud (el tamaño) del intervalo modal.

Ventajas de la Moda

• Es fácil de calcular.
• Es muy clara de entender.
• Se puede usar con datos que no son números (como colores, nombres, etc.), lo cual no es posible con la media o la mediana.
• Es útil para describir las características más comunes de un grupo.

Desventajas de la Moda

• Su valor puede cambiar mucho si se añaden o quitan pocos datos.
• Cuando los datos están agrupados en intervalos, su valor puede depender de cómo se agrupen los datos.
• No siempre se encuentra en el centro de todos los datos.
• Puede haber más de una moda, lo que a veces complica su interpretación.

Véase también

En inglés: Mode (statistics) Facts for Kids

• Frecuencia
• Frecuencia estadística
• Media
• Mediana
• Parámetro estadístico
• Valor esperado
• Medidas de tendencia central

Galería de imágenes

• 

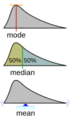
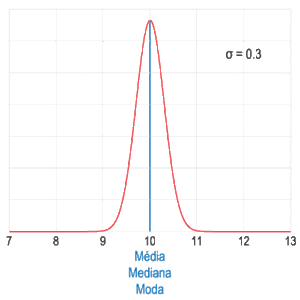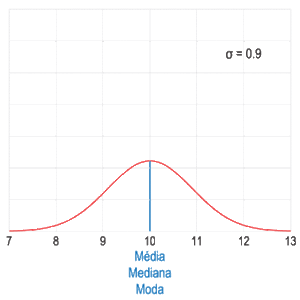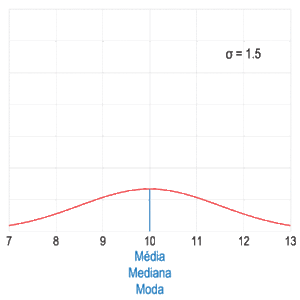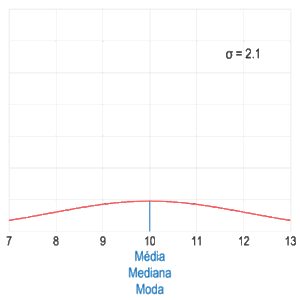
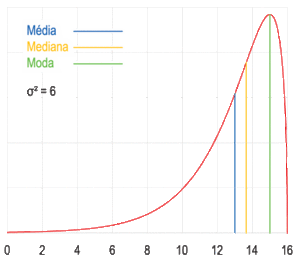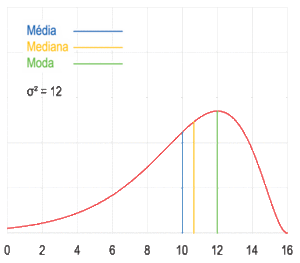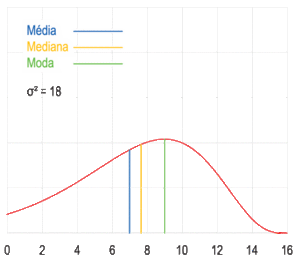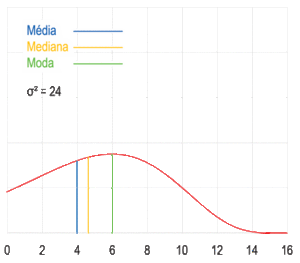
  Visualización geométrica de la moda, la mediana y de la media de una función arbitraria de densidad de probabilidad.