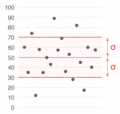
Parámetro estadístico para niños
En estadística, un parámetro es un número especial que nos ayuda a entender un grupo grande de información. Imagina que tienes muchos datos sobre algo, como las edades de todos los estudiantes de una escuela. En lugar de mirar cada edad por separado, un parámetro te da un resumen, como la edad promedio de todos.
Estos números son muy útiles porque nos permiten crear un "modelo" o una forma sencilla de entender la realidad. Si tuviéramos que revisar cada dato individualmente, sería muy complicado. Los parámetros nos ayudan a resumir, comparar grupos, ver si los datos se ajustan a una idea y tomar decisiones.
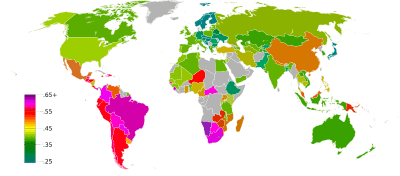
Por ejemplo, para saber si una población es "joven", podemos calcular la edad promedio de sus habitantes. Esto se hace sumando todas las edades y dividiendo el resultado por el número total de personas.
Contenido
- ¿Qué es un Parámetro Estadístico?
- Cualidades de un Buen Parámetro
- Tipos Principales de Parámetros
- Parámetros Bidimensionales
- Parámetros en la Inferencia Estadística
- Galería de imágenes
- Véase también
¿Qué es un Parámetro Estadístico?
Un parámetro estadístico es una medida que describe a toda una población. Piensa en ello como una forma de medir algo en un grupo completo. Por ejemplo, la estatura promedio de todos los niños de 12 años en tu ciudad sería un parámetro.
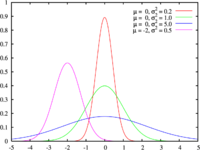
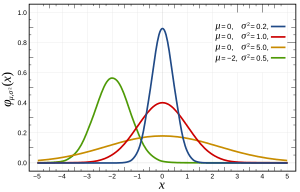
En matemáticas más avanzadas, un parámetro también puede ser una variable que ayuda a definir cómo se comportan ciertos modelos. Por ejemplo, en un tipo de distribución llamada "normal", hay parámetros que nos dicen cómo se distribuyen los datos, como dónde está el centro o qué tan dispersos están.
Cualidades de un Buen Parámetro
Para que un parámetro sea realmente útil, debe tener ciertas características:
- Debe ser claro y objetivo: Su cálculo debe ser preciso, generalmente con una fórmula matemática. Por ejemplo, la media (promedio) se calcula sumando todos los datos y dividiendo por el total. No hay dudas sobre cómo obtenerla.
- Debe usar la mayor cantidad de datos posible: Un parámetro es más representativo si se basa en muchos datos. Cuantos más datos se usen, mejor reflejará la realidad del grupo.
- Debe ser fácil de entender: Su significado debe ser claro. Por ejemplo, la mediana nos dice que la mitad de los datos están por debajo de ese valor y la otra mitad por encima.
- Debe ser sencillo de calcular: Es mejor si se puede calcular fácilmente y usar en otras operaciones matemáticas.
- Debe ser estable: Si tomas diferentes muestras pequeñas del mismo grupo, el parámetro no debería cambiar mucho. Esto significa que representa bien a todo el grupo.
Tipos Principales de Parámetros
Los parámetros se agrupan en diferentes categorías según lo que miden:
- Medidas de tendencia central: Nos dicen dónde está el "centro" de los datos.
- Medidas de posición no central: Nos indican la posición de un dato dentro del grupo.
- Medidas de dispersión: Nos muestran qué tan separados o juntos están los datos.
- Medidas de forma: Describen la forma de la gráfica de los datos.
Además, hay otros parámetros para situaciones específicas, como las proporciones o las tasas.
Medidas de Tendencia Central
Estas medidas nos dan un valor que suele estar en el centro de cómo se distribuyen los datos. Las más conocidas son la media (promedio), la moda y la mediana.
¿Qué es la Media Aritmética o Promedio?
La media aritmética, o promedio, es uno de los parámetros más comunes. Se calcula sumando todos los datos y dividiendo por el número total de datos.
- Fácil de calcular: Se usan todos los datos para obtenerla.
- Punto de equilibrio: Se puede ver como el "centro de equilibrio" de los datos.
- Sensibilidad: La media puede verse muy afectada por valores extremos (muy grandes o muy pequeños). Por ejemplo, si en un equipo de baloncesto hay un jugador muy alto, la estatura promedio podría ser alta, pero no representaría bien a la mayoría de los jugadores.
¿Qué es la Moda?
La moda es el dato que más se repite en un conjunto de valores. Es como decir "lo que está de moda", es lo más frecuente.
- Cálculo sencillo: Solo necesitas contar cuál es el dato que aparece más veces.
- Interpretación clara: Es fácil de entender.
- Útil para datos cualitativos: Se puede usar para cosas que no son números, como el color de ojos más común en un grupo.
Sin embargo, la moda puede no estar siempre en el centro de los datos y a veces puede haber más de una moda.
¿Qué es la Mediana?
La mediana es el valor que se encuentra justo en el medio de un conjunto de datos cuando estos están ordenados de menor a mayor. La mitad de los datos son menores que la mediana y la otra mitad son mayores.
- Menos sensible a valores extremos: A diferencia de la media, la mediana no se ve tan afectada por datos muy grandes o muy pequeños. Esto la hace muy útil para resumir información como los salarios, donde unos pocos salarios muy altos podrían distorsionar el promedio.
- Fácil de interpretar: Nos dice que la mitad de las personas ganan más que la mediana y la otra mitad ganan menos.
Medidas de Posición No Central
Estas medidas, también llamadas cuantiles, son una extensión de la mediana. Nos dicen qué valor deja por debajo de sí una cierta cantidad de datos.
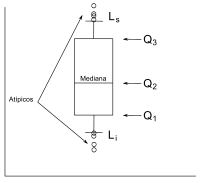
- Cuartiles: Dividen los datos en cuatro partes iguales. El primer cuartil deja el 25% de los datos por debajo, el segundo es la mediana (50%), y el tercer cuartil deja el 75% por debajo.
- Deciles: Dividen los datos en diez partes.
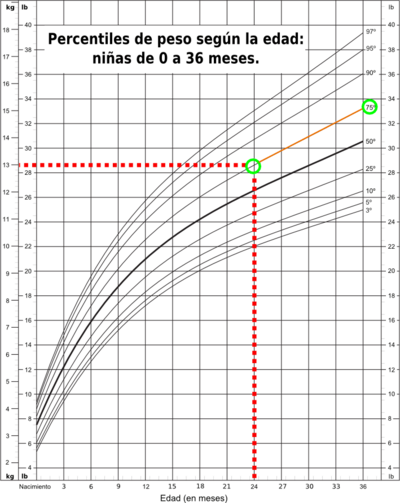
- Percentiles: Dividen los datos en cien partes. Si alguien está en el percentil 75 en una prueba, significa que el 75% de las personas obtuvieron una puntuación más baja que él.
Comentarios sobre las Medidas de Posición
Es importante elegir el parámetro adecuado para cada situación. Por ejemplo, si el salario promedio de una empresa es de 1600 €, podría ser que cuatro empleados ganen 1000 € y el jefe gane 4000 €. La media es 1600 €, pero no representa lo que gana la mayoría. En este caso, la mediana podría ser más útil.
En general, la media es buena si los datos son bastante parecidos. Si los datos son muy diferentes, la mediana es mejor. La moda es la única opción si los datos son categorías (como colores o tipos de mascotas).
Medidas de Dispersión
Mientras que las medidas de posición nos dicen dónde está el centro, las medidas de dispersión nos informan sobre qué tan "extendidos" o "juntos" están los datos. Nos ayudan a entender si los datos son muy parecidos entre sí o si varían mucho.
Medidas de Dispersión Absolutas
- Recorrido o Rango: Es la diferencia entre el valor más alto y el más bajo de los datos. Es simple, pero solo usa dos valores.
- Desviaciones Medias: Miden qué tan lejos está cada dato de un valor central (como la media o la mediana).
- Varianza y Desviación Típica: Son las medidas de dispersión más usadas. La varianza se calcula promediando las diferencias al cuadrado de cada dato respecto a la media. La desviación típica es la raíz cuadrada de la varianza. Nos dicen cuánto se desvían los datos de la media. Si la desviación típica es pequeña, los datos están muy juntos; si es grande, están muy dispersos.
Medidas de Dispersión Relativas
Estas medidas nos dan la dispersión en términos de porcentaje o proporción, lo que facilita comparar la dispersión entre diferentes grupos de datos.
- Coeficiente de Variación de Pearson: Compara la desviación típica con la media. Nos dice qué tan variable es un grupo de datos en relación con su promedio.
- Coeficiente de Apertura: Se usa para comparar salarios en empresas, por ejemplo.
- Recorridos Relativos: Son versiones relativas del rango y el rango intercuartílico.
Medidas de Forma
Estas medidas describen la forma de la gráfica de una distribución de datos. A menudo se comparan con la "campana de Gauss", que es la forma de la distribución normal, muy común en la naturaleza.
Medidas de Asimetría
Una distribución es simétrica si, al trazar una línea vertical por su centro, las dos mitades son un espejo. Si no es simétrica, decimos que tiene asimetría. La posición de la media, mediana y moda nos puede dar una idea de la asimetría.
Medidas de Apuntamiento o Curtosis
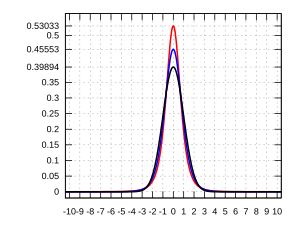
Estas medidas nos dicen qué tan "picuda" o "aplastada" es la gráfica de una distribución en comparación con la campana de Gauss.
- Platicúrticas: Más aplastadas que la normal.
- Mesocúrticas: Igual de apuntadas que la normal.
- Leptocúrticas: Más picudas que la normal.
Otros Parámetros Importantes
Hay otros parámetros que se usan en situaciones específicas y son muy útiles para resumir información:
Proporción
La proporción de un dato es cuántas veces aparece ese dato en relación con el total de datos. También se le llama frecuencia relativa. Por ejemplo, si en un grupo de 20 personas, 7 tienen ojos azules, la proporción de ojos azules es del 35%.
Número Índice
Un número índice nos ayuda a ver cómo cambian las cosas con el tiempo o en diferentes lugares. Un ejemplo común es el índice de precios al consumidor (IPC), que nos dice cómo cambian los precios de los productos con el tiempo.
Tasa
Una tasa es una medida que relaciona la cantidad de un fenómeno con su frecuencia. Se usa para cosas que no se pueden medir directamente. Ejemplos son la tasa de natalidad (cuántos nacimientos hay) o la tasa de desempleo (cuántas personas no tienen trabajo).
Coeficiente de Gini
El coeficiente de Gini mide la desigualdad o la concentración de algo, como los salarios. Nos dice qué tan equitativamente se distribuye el dinero en un grupo. Un valor bajo significa que el dinero está más repartido, y un valor alto significa que está más concentrado en pocas manos.
Parámetros Bidimensionales
A veces, en estadística, estudiamos dos características al mismo tiempo para ver si están relacionadas. Por ejemplo, la estatura y el peso de las personas. Para esto, usamos parámetros bidimensionales.
Centro de Gravedad
Si graficamos los datos de dos variables (como estatura y peso), el centro de gravedad es el punto que representa el promedio de ambas variables. Es como el "punto de equilibrio" de todos los datos.
Covarianza
La covarianza nos dice si dos variables se mueven en la misma dirección. Si la covarianza es positiva, significa que cuando una variable aumenta, la otra también tiende a aumentar. Si es negativa, cuando una aumenta, la otra tiende a disminuir.
Coeficiente de Correlación Lineal
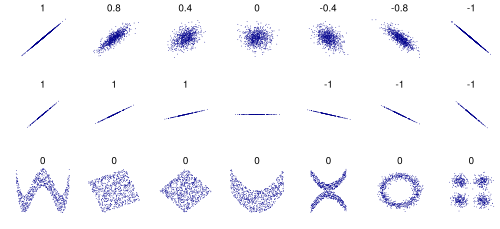
Este coeficiente nos ayuda a saber qué tan fuerte es la relación lineal entre dos variables. Su valor va de -1 a 1.
- Si está cerca de 1 o -1, la relación es fuerte.
- Si está cerca de 0, la relación es débil o no existe.
Parámetros en la Inferencia Estadística
A veces no podemos estudiar a toda la población (por ejemplo, si es muy grande o si el estudio la dañaría). En esos casos, tomamos una pequeña parte de la población, llamada muestra. Usamos los datos de la muestra para estimar los parámetros de toda la población.
Aquí distinguimos entre:
- Parámetro: Un número que describe a toda la población.
- Estadístico: Un número que describe a una muestra.
Por ejemplo, la media de una muestra se llama "media muestral", y la usamos para estimar la "media poblacional".
Galería de imágenes
-
La media aritmética como resumen de la vejez de un país.
-
Conjunto de datos estadísticos de media aritmética 50 (línea azul) y desviación típica 20 (líneas rojas).
-
Posiciones relativas de los parámetros de centralización en distribuciones simétricas y asimétricas.
-
Ejemplos de formas de distribución.
Véase también
En inglés: Statistical parameter Facts for Kids
