Mayor número primo conocido para niños
El mayor número primo conocido es el número entero más grande que los matemáticos han descubierto hasta ahora que cumple con la condición de ser un número primo. Un número primo es un número natural mayor que 1 que solo se puede dividir exactamente por 1 y por sí mismo. Por ejemplo, 2, 3, 5, 7 y 11 son números primos.
Actualmente, el mayor número primo conocido es el 2136.279.841 − 1. Este número es gigantesco, ¡tiene más de 41 millones de dígitos! Para que te hagas una idea, si lo escribiéramos, ocuparía miles de páginas. Fue descubierto en octubre de 2024 por un ordenador que participaba en un proyecto llamado Gran Búsqueda de Primos de Mersenne en Internet (GIMPS).
El famoso matemático griego Euclides demostró hace mucho tiempo que existen infinitos números primos. Esto significa que, por muy grande que sea el número primo que encontremos, siempre habrá uno aún mayor esperando ser descubierto. Por eso, muchas personas, tanto matemáticos profesionales como aficionados, disfrutan buscando estos números gigantes.
La Electronic Frontier Foundation incluso ofrece premios a quienes encuentran números primos que rompen récords.
Contenido
¿Qué son los Primos de Mersenne?
Los números de Mersenne son un tipo especial de números primos que tienen una forma particular: 2p − 1, donde 'p' también es un número primo. Por ejemplo, si p=3, 23 - 1 = 8 - 1 = 7, que es un número primo.
¿Por qué son importantes los Primos de Mersenne?
Encontrar números primos muy grandes es un desafío. Sin embargo, para los números de Mersenne, existen pruebas especiales que son muy rápidas. Una de ellas es la prueba de primalidad de Lucas-Lehmer. Gracias a esto, y al interés histórico que han tenido, la mayoría de los números primos más grandes que se han descubierto son primos de Mersenne.
De hecho, hasta hace poco, casi todos los récords de números primos más grandes eran de este tipo. Los últimos catorce récords descubiertos han sido primos de Mersenne.
La búsqueda de números primos con computadoras
El uso de ordenadores ha cambiado por completo la búsqueda de números primos. Desde 1951, todos los récords de números primos más grandes se han encontrado con la ayuda de computadoras.
En 1999, el número primo más grande conocido superó el millón de dígitos, y esto le valió a sus descubridores un premio de 50.000 dólares. En 2008, el récord superó los diez millones de dígitos, lo que fue premiado con 100.000 dólares. También se han ofrecido premios para el primer número primo que tenga al menos cien millones de dígitos y para el primero que tenga mil millones de dígitos.
El proyecto GIMPS, que ha encontrado los últimos 11 récords, funciona gracias a miles de ordenadores de personas comunes de todo el mundo. Estas personas instalan un programa especial en sus computadoras que las ayuda a buscar estos números gigantes cuando no están en uso.
| Posición | Número primo | Encontrado por | Fecha en que fue encontrado |
Número de dígitos |
|---|---|---|---|---|
| 1.º | 2136.279.841 − 1 | GIMPS | 12 de octubre de 2024 | 41 024 320 |
| 2.º | 282.589.933 − 1 | GIMPS | 7 de diciembre de 2018 | 24 862 048 |
| 3.º | 277.232.917 − 1 | GIMPS | 26 de diciembre de 2017 | 23 249 425 |
| 4.º | 274.207.281 − 1 | GIMPS | 7 de enero de 2016 | 22 338 618 |
| 5.º | 257.885.161 − 1 | GIMPS | 25 de enero de 2013 | 17 425 170 |
| 6.º | 243.112.609 − 1 | GIMPS | 23 de agosto de 2008 | 12 978 189 |
| 7.º | 242.643.801 − 1 | GIMPS | 12 de abril de 2009 | 12 837 064 |
| 8.º | 237.156.667 − 1 | GIMPS | 6 de septiembre de 2008 | 11 185 272 |
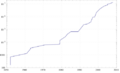
Historia de los récords de números primos
La siguiente tabla muestra algunos de los mayores números primos conocidos a lo largo de la historia. La notación Mn se refiere a un número de Mersenne con exponente n.
| Número | Dígitos | Año en que fue encontrado |
|---|---|---|
| M127 | 39 | 1876 |
| 180×(M127)2+1 | 79 | 1951 |
| M521 | 157 | 1952 |
| M607 | 183 | 1952 |
| M1279 | 386 | 1952 |
| M2203 | 664 | 1952 |
| M2281 | 687 | 1952 |
| M3217 | 969 | 1957 |
| M4423 | 1332 | 1961 |
| M9689 | 2917 | 1963 |
| M9941 | 2993 | 1963 |
| M11213 | 3376 | 1963 |
| M19937 | 6002 | 1971 |
| M21701 | 6533 | 1978 |
| M23209 | 6987 | 1979 |
| M44497 | 13395 | 1979 |
| M86243 | 25 962 | 1982 |
| M132049 | 39 751 | 1983 |
| M216091 | 65 050 | 1985 |
| M216193 | 65 087 | 1989 |
| M756839 | 227 832 | 1992 |
| M859433 | 258 716 | 1994 |
| M1257787 | 378 632 | 1996 |
| M1398269 | 420 921 | 1996 |
| M2976221 | 895 932 | 1997 |
| M3021377 | 909 526 | 1998 |
| M6972593 | 2 098 960 | 1999 |
| M13466917 | 4 053 946 | 2001 |
| M20996011 | 6 320 430 | 2003 |
| M24036583 | 7 235 733 | 2004 |
| M25964951 | 7 816 230 | 2005 |
| M30402457 | 9 152 052 | 2005 |
| M32582657 | 9 808 358 | 2006 |
| M43112609 | 12 978 189 | 2008 |
| M57885161 | 17 425 170 | 2013 |
| M74207281 | 22 338 618 | 2016 |
| M77232917 | 23 249 425 | 2017 |
| M82589933 | 24 862 048 | 2018 |
| M136279841 | 41 024 320 | 2024 |
Galería de imágenes
Véase también
 En inglés: Largest known prime number Facts for Kids
En inglés: Largest known prime number Facts for Kids