Margen de error para niños
El margen de error (MDE) es una medida que nos dice cuánto podría variar un resultado. Se usa mucho en encuestas para saber qué tan cerca está el resultado de la verdad. También lo usamos en la vida diaria para hablar de la flexibilidad que tenemos para lograr algo. Por ejemplo, en los deportes, se usa para describir la precisión necesaria. Imagina que un jugador de bolos necesita golpear un bolo específico; el margen de error sería el espacio extra que tiene la bola para desviarse y aun así golpearlo.
Contenido
Margen de Error: ¿Qué es y por qué es importante?
El margen de error es clave para entender la fiabilidad de los datos, especialmente en las encuestas. Nos ayuda a saber si un resultado es muy preciso o si podría cambiar bastante.
Entendiendo el Margen de Error
Imagina que haces una encuesta sencilla de "sí" o "no" a un grupo de personas. Obtienes un porcentaje de respuestas "sí". El margen de error nos ayuda a saber qué tan cerca está ese porcentaje del resultado real si le preguntaras a todas las personas de la población.
Si repitieras la misma encuesta muchas veces con diferentes grupos, los resultados serían un poco distintos cada vez. El margen de error nos dice dentro de qué rango se espera que caigan la mayoría de esos resultados.
Por ejemplo, si una encuesta dice que el 50% de las personas prefiere algo con un margen de error del 3%, significa que el porcentaje real podría estar entre el 47% y el 53%. Esto se conoce como el intervalo de confianza.
¿Cómo se usa en la vida diaria?
El margen de error no solo se aplica a las encuestas. También lo usamos para hablar de la precisión en otras situaciones. Por ejemplo, un ingeniero que construye un puente debe calcular el margen de error para asegurarse de que la estructura sea segura y resista diferentes condiciones. En un juego, el margen de error puede ser la cantidad de espacio que tienes para cometer un pequeño fallo sin perder.
Margen de Error en las Encuestas
Cuando ves los resultados de una encuesta, el margen de error es un dato muy importante. Nos indica la posible variación de los resultados debido a que solo se preguntó a una parte de la población, no a todos.
¿Qué es el nivel de confianza?
El margen de error siempre va acompañado de un "nivel de confianza". El más común es el 95%. Esto significa que si repitieras la encuesta 100 veces, en 95 de ellas el resultado real de la población estaría dentro del margen de error que se calculó.
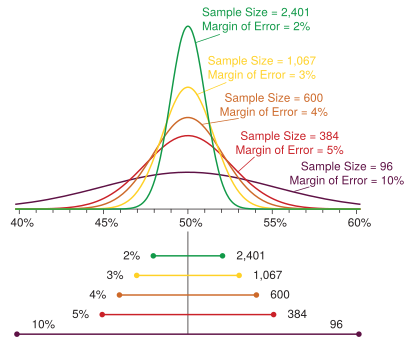
¿Cómo afecta el tamaño de la muestra?
El tamaño de la muestra es el número de personas encuestadas. Cuantas más personas se encuesten, más pequeño será el margen de error. Esto tiene sentido, ¿verdad? Si preguntas a más gente, tu resultado será más cercano a la realidad.
Por ejemplo:
- Para un 95% de confianza, si encuestas a 400 personas, el margen de error es de aproximadamente ±4.9%.
- Si encuestas a 1600 personas, el margen de error baja a aproximadamente ±2.45%.
- Si encuestas a 10,000 personas, el margen de error es de aproximadamente ±0.98%.
Como puedes ver, aumentar mucho el número de encuestados reduce el margen de error, haciendo el resultado más preciso.
¿Por qué el 50% tiene el mayor margen de error?
En una encuesta con opciones de "sí" o "no", el margen de error es más grande cuando el resultado está cerca del 50%. Si un resultado es, por ejemplo, 71% o 2%, el margen de error será más pequeño. Esto se debe a cómo se calculan las probabilidades en estadística. Por eso, el margen de error que se suele informar en las noticias es el "margen de error máximo", que es el que se daría si el resultado fuera 50%.
¿Importa el tamaño de la población?
Generalmente, la fórmula del margen de error asume que la población es muy grande. Esto significa que el tamaño de la población no suele afectar el margen de error, siempre y cuando la muestra sea una pequeña parte de esa población (menos del 5%). Si la muestra es muy grande en comparación con la población, se puede hacer un pequeño ajuste para que el margen de error sea aún más preciso. Si encuestaras a toda la población, el margen de error sería cero, ¡porque ya sabrías el resultado exacto!
Comparando resultados de encuestas
A veces, las encuestas muestran que dos candidatos o dos opciones tienen resultados muy parecidos. Si la diferencia entre ellos es menor que el margen de error, se dice que hay un "empate estadístico". Esto significa que, según la encuesta, no podemos decir con seguridad quién va ganando, ya que la diferencia podría deberse al azar del muestreo.
Es importante recordar que el margen de error se aplica a cada porcentaje individual, no directamente a la diferencia entre dos porcentajes. Comparar porcentajes requiere un análisis un poco más complejo.
Galería de imágenes
-
Representación visual de la regla empírica basada en la distribución normal.
-
Gráficas que muestran cómo el margen de error cambia con el tamaño de la muestra y el nivel de confianza.
Véase también
En inglés: Margin of error Facts for Kids
- Error de medición
- Error experimental
- Medidas de dispersión
