Gnomon para niños
El gnomon (del griego γνώμων, que significa 'guía' o 'maestro') es una pieza alargada que proyecta una sombra sobre una superficie marcada. Esta sombra se usa para medir el paso del tiempo, como en los relojes de sol.
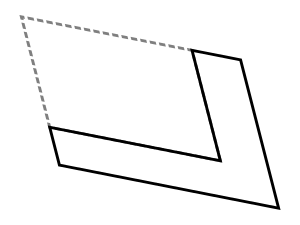
En el campo de las matemáticas, los antiguos griegos también usaban la palabra gnomon para describir una forma geométrica. Se referían a ella como la figura que queda cuando quitas un cuadrado más pequeño de la esquina de un cuadrado más grande. Otra forma de verlo, según el filósofo Aristóteles, es una figura que, al añadirla a un cuadrado, hace que sus lados crezcan, pero la forma general del cuadrado no cambia. Más tarde, el matemático Euclides amplió esta idea para aplicarla a otras figuras geométricas llamadas paralelogramos.
Contenido
¿Cómo funciona un gnomon en un reloj de sol?
El gnomon, también llamado estilo, es la parte de un reloj de sol que proyecta la sombra. Su posición es muy importante para que el reloj funcione correctamente. Generalmente, el gnomon se inclina con un ángulo que es igual a la latitud del lugar donde se encuentra el reloj. La latitud es la distancia de un lugar al ecuador.
En el hemisferio norte (la parte de la Tierra al norte del ecuador), el borde del gnomon que proyecta la sombra apunta hacia el norte. De esta manera, queda paralelo al eje de rotación de la Tierra, que es la línea imaginaria alrededor de la cual gira nuestro planeta.
¿Quién usó el gnomon para medir la Tierra?
Hace mucho tiempo, un sabio griego llamado Eratóstenes de Cirene usó un gnomon para calcular el diámetro de la Tierra. ¡Lo hizo con una precisión sorprendente para su época!
El gnomon en la geometría y los números
En geometría, un gnomon es una figura que, cuando se añade a otra figura original, crea una nueva figura que es similar a la original. Esto significa que la nueva figura tiene la misma forma, pero es más grande.
Por ejemplo, si tienes un rectángulo especial llamado "rectángulo áureo", su gnomon es un cuadrado. Cuando añades ese cuadrado al rectángulo, obtienes un rectángulo áureo más grande. Otro ejemplo son los tamaños de papel como A0, A1, A2, A3, A4, etc. Estos tamaños se obtienen dividiendo por la mitad el lado más largo del tamaño anterior. El gnomon en este caso es otro rectángulo del mismo tipo.
En la aritmética antigua, el gnomon también se usaba para entender cómo crecen los números. Por ejemplo, en los números cuadrados (como 4, 9, 16, 25...), el gnomon es la cantidad de unidades que necesitas añadir a un número cuadrado para obtener el siguiente. Para pasar del 4 al 9, necesitas añadir 5 unidades. Así, el gnomon del 4 es el 5. Para esta serie de números, se descubrió que los gnomones son los números impares (3, 5, 7, 9...). Esto demuestra que el gnomon ayuda a que una figura o un número crezca sin cambiar su forma o patrón esencial.
Galería de imágenes
-
El gnomon es la pieza triangular de este reloj de sol.
-
Gnomon triangular.
-
Gnomon en matemáticas
Véase también
En inglés: Gnomon Facts for Kids
