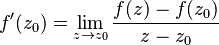Función holomorfa para niños

Las funciones holomorfas son un tipo especial de funciones que se estudian en una rama de las matemáticas llamada análisis complejo. Estas funciones trabajan con números complejos, que son números que tienen una parte "real" y una parte "imaginaria".

Imagina que tienes un mapa donde cada punto es un número complejo. Una función holomorfa es como una regla que toma un número complejo de ese mapa y lo transforma en otro número complejo. Lo especial de estas funciones es que son muy "suaves" y "predecibles" en su comportamiento. Esto significa que, si te acercas a un punto en el mapa, la forma en que la función cambia es siempre la misma, sin importar desde qué dirección te acerques.

Esta característica de ser "suave" y "predecible" es mucho más fuerte que la idea de "suavidad" que usamos para funciones con números normales (reales). Gracias a esta propiedad, las funciones holomorfas se pueden describir con mucha precisión usando algo llamado serie de Taylor, que es como una suma infinita de términos que se acercan cada vez más al valor de la función.

A veces, a las funciones holomorfas también se les llama funciones analíticas o funciones regulares. Si una función holomorfa está definida en todo el plano complejo (es decir, en todos los números complejos), se le llama función entera.

¿Qué significa que una función sea holomorfa?

Gráfico tridimensional del valor absoluto de la función gamma compleja.

Para entender qué es una función holomorfa, primero necesitamos saber qué significa que una función sea "diferenciable" en el mundo de los números complejos.

Imagina que tienes una función que transforma números complejos. La "derivada" de esa función en un punto específico nos dice cómo cambia la función justo en ese punto. Es como la pendiente de una curva, pero en un espacio más complejo.

La definición matemática de la derivada de una función f en un punto z₀ es:

Esto significa que, a medida que el número z se acerca mucho a z₀, la división de la diferencia entre los valores de la función y la diferencia entre los números mismos, debe acercarse siempre al mismo número, sin importar cómo se acerque z a z₀.

Una función es holomorfa en un área (un "conjunto abierto") si es "diferenciable compleja" en cada punto de esa área. Si una función es holomorfa en un punto z₀, significa que es holomorfa en una pequeña región alrededor de z₀.

Es importante saber que una función puede ser diferenciable en un solo punto, pero no ser holomorfa en ese punto. Por ejemplo, la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(z)=|z|^2 es diferenciable en el número 0, pero no en otros puntos. Por eso, no es holomorfa en 0.

Las funciones holomorfas tienen propiedades similares a las funciones diferenciables con números reales, como las reglas para derivar sumas, productos y divisiones.

Origen del término

El término holomorfo fue creado en 1875 por los matemáticos Charles Briot y Jean-Claude Bouquet. Viene de dos palabras griegas: hólos, que significa "todo", y morphḗ, que significa "forma" o "tipo". Esto se usa en contraste con el término meromorfa, que viene de méros, que significa "parte".

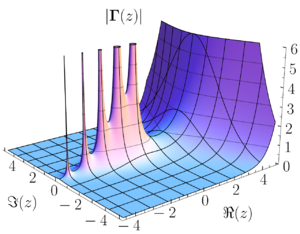
La idea es que una función holomorfa se comporta de manera "completa" o "entera" en un área del plano complejo, mientras que una función meromorfa se comporta como una "parte" o una fracción de funciones holomorfas, ya que puede tener algunos puntos donde no está definida (llamados "polos").

Ejemplos de funciones holomorfas

Algunos ejemplos de funciones holomorfas son:

• Todas las funciones polinómicas con números complejos (como z², z³ + 5z, etc.).
• Las funciones trigonométricas (como seno y coseno de z).
• La función exponencial (como e^z).
• La función logaritmo (ln(z)) es holomorfa en la mayoría de los números complejos, excepto en los números reales negativos y el cero.
• La función 1/z es holomorfa en todos los números complejos excepto en el 0.

Características importantes

Las funciones holomorfas tienen varias propiedades interesantes:

• Operaciones básicas: Si sumas, restas, multiplicas o divides dos funciones holomorfas, el resultado también será una función holomorfa (siempre que no dividas por cero).
• Composición: Si aplicas una función holomorfa y luego otra función holomorfa al resultado, la función combinada también será holomorfa.
• Suavidad infinita: Una función holomorfa es infinitamente diferenciable en cada punto. Esto significa que puedes calcular su derivada, la derivada de su derivada, y así sucesivamente, infinitas veces. Además, se puede representar perfectamente con su serie de Taylor.
• Relación con funciones armónicas: Las funciones holomorfas se pueden dividir en una parte real y una parte imaginaria. Cada una de estas partes es una función armónica, lo que significa que satisfacen una ecuación especial llamada ecuación de Laplace.
• Teorema integral de Cauchy: Este teorema dice que los valores de una función holomorfa dentro de un círculo están completamente determinados por los valores de la función en el borde de ese círculo. Es como si el borde "controlara" todo lo que pasa dentro.
• Fórmula integral de Cauchy: Esta fórmula nos da una manera explícita de calcular el valor de una función holomorfa en cualquier punto dentro de un círculo, usando solo los valores de la función en el borde del círculo.
• Preservación de ángulos: En las regiones donde su derivada no es cero, las funciones holomorfas son "conformes". Esto significa que preservan los ángulos y la forma de las figuras pequeñas, aunque pueden cambiar su tamaño.

Galería de imágenes

• 

  La función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(z) = \bar z no es diferenciable compleja en cero.

Véase también

En inglés: Holomorphic function Facts for Kids

• Biholomorfismo
• Función meromorfa