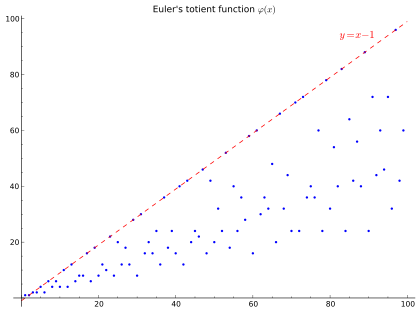
Función φ de Euler para niños

La función φ (phi) de Euler es un concepto muy interesante en las matemáticas, especialmente en una rama llamada teoría de números. Imagina que tienes un número entero positivo, por ejemplo, el 10. La función φ(10) te dirá cuántos números enteros positivos menores que 10 no comparten ningún factor común con 10, excepto el 1.

Estos números que solo comparten el 1 como factor común se llaman números coprimos. Por ejemplo, para el 10, los números menores que él son 1, 2, 3, 4, 5, 6, 7, 8, 9.

• El 1 es coprimo con 10.
• El 2 no es coprimo con 10 (ambos son divisibles por 2).
• El 3 es coprimo con 10.
• El 4 no es coprimo con 10 (ambos son divisibles por 2).
• El 5 no es coprimo con 10 (ambos son divisibles por 5).
• El 6 no es coprimo con 10 (ambos son divisibles por 2).
• El 7 es coprimo con 10.
• El 8 no es coprimo con 10 (ambos son divisibles por 2).
• El 9 es coprimo con 10.

Así, los números coprimos con 10 y menores que él son 1, 3, 7 y 9. Hay 4 de ellos. Entonces, φ(10) = 4.

Esta función es muy útil en matemáticas y tiene aplicaciones importantes, como en la seguridad de la información en internet.

Historia y nombres

Los primeros mil valores de .

El famoso matemático Leonhard Euler introdujo esta función en 1763. Al principio, no usó un símbolo especial para ella. Más tarde, en 1784, la estudió más a fondo y usó la letra griega π (pi) para representarla.

La notación que usamos hoy, φ(A), viene del matemático Carl Friedrich Gauss en su libro de 1801, Disquisitiones arithmeticae. Por eso, a menudo se le llama función phi de Euler o simplemente función phi.

En 1879, otro matemático, James Joseph Sylvester, le dio el nombre de totiente. Por eso, también se la conoce como función totiente de Euler.

Cómo calcular la función phi

Calcular la función φ(n) es más fácil de lo que parece si conoces algunas reglas:

• Para el número 1: φ(1) = 1. Esto es porque el 1 es coprimo consigo mismo.

• Si 'p' es un número primo: φ(p) = p - 1.

* Un número primo solo tiene dos divisores: 1 y él mismo. Por ejemplo, para el 7 (que es primo), todos los números menores que 7 (1, 2, 3, 4, 5, 6) son coprimos con él. Así que φ(7) = 7 - 1 = 6.

• Si 'p' es un número primo y 'k' es un número entero positivo: φ(p^k) = (p - 1)p^{k - 1}.

* Por ejemplo, para φ(3²) = φ(9): * Los números menores o iguales a 9 que NO son coprimos con 9 son los múltiplos de 3: 3, 6, 9. Hay 3 de ellos. * El total de números es 9. * Entonces, los coprimos son 9 - 3 = 6. * Usando la fórmula: φ(3²) = (3 - 1) * 3^{(2 - 1)} = 2 * 3¹ = 6. ¡Coincide!

• Si 'm' y 'n' son números coprimos: φ(mn) = φ(m) * φ(n). Esta propiedad se llama "multiplicativa".

* Por ejemplo, φ(10) = φ(2 * 5). Como 2 y 5 son primos y, por lo tanto, coprimos: * φ(2) = 2 - 1 = 1 * φ(5) = 5 - 1 = 4 * Entonces, φ(10) = φ(2) * φ(5) = 1 * 4 = 4. ¡Funciona!

Fórmula general

Gracias a estas propiedades, podemos calcular φ(n) para cualquier número 'n' si conocemos sus factores primos. El Teorema Fundamental de la Aritmética dice que cualquier número entero mayor que 1 se puede escribir como una multiplicación de números primos.

Si 'n' se escribe como: n = p₁^k₁ * p₂^k₂ * ... * p_r^k_r (donde p₁, p₂, etc., son números primos diferentes y k₁, k₂, etc., son sus potencias), entonces la fórmula para φ(n) es:

φ(n) = (p₁ - 1)p₁^{k₁ - 1} * ... * (p_r - 1)p_r^{k_r - 1}.

También se puede escribir como la Fórmula de Producto de Euler: φ(n) = n * (1 - 1/p₁) * (1 - 1/p₂) * ... * (1 - 1/p_r)

Ejemplo de cálculo

Calculemos φ(36). Primero, encontramos los factores primos de 36: 36 = 2² * 3². Aquí, p₁ = 2, k₁ = 2 y p₂ = 3, k₂ = 2.

Usando la primera fórmula: φ(36) = (2 - 1)2^{(2 - 1)} * (3 - 1)3^{(2 - 1)} φ(36) = (1) * 2¹ * (2) * 3¹ φ(36) = 1 * 2 * 2 * 3 = 12.

Usando la Fórmula de Producto de Euler: φ(36) = 36 * (1 - 1/2) * (1 - 1/3) φ(36) = 36 * (1/2) * (2/3) φ(36) = 36 * (2/6) = 36 * (1/3) = 12.

Podemos verificarlo manualmente. Los números coprimos con 36 (que no son divisibles por 2 ni por 3) y menores que 36 son: 1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31 y 35. ¡Hay 12 de ellos!

Algunos valores

Representación gráfica de los 100 primeros valores.

Aquí tienes una tabla con los primeros valores de la función φ(n):

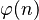	+0	+1	+2	+3	+4	+5	+6	+7	+8	+9
0+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60

Teorema de Euler

El Teorema de Euler es muy importante y dice lo siguiente: si 'a' y 'n' son números coprimos, entonces 'a' elevado a la potencia φ(n) es equivalente a 1 cuando se divide por 'n'. Esto se escribe así: 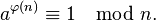Un caso especial de este teorema, cuando 'n' es un número primo, se conoce como el pequeño teorema de Fermat.

Este teorema es la base de sistemas de seguridad muy importantes, como el RSA.

Aplicaciones de la función phi

Construcción de polígonos

En su libro Disquisitiones arithmeticae, Gauss demostró que se puede construir un polígono regular de 'n' lados usando solo una regla y un compás si φ(n) es una potencia de 2 (es decir, 2, 4, 8, 16, etc.).

Por ejemplo, si 'n' es una potencia de un número primo impar, φ(n) solo será una potencia de 2 si 'n' es un número primo de Fermat. Los números primos de Fermat son primos que son uno más que una potencia de 2. Solo se conocen cinco de ellos: 3, 5, 17, 257 y 65537.

Esto significa que un polígono regular de 'n' lados se puede construir con regla y compás si 'n' es el producto de números primos de Fermat diferentes y cualquier potencia de 2. Algunos de estos 'n' son: 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40...

El sistema de seguridad RSA

El RSA es un sistema de seguridad que se usa para proteger la información en internet, como cuando haces compras en línea o envías mensajes privados. La función φ(n) es clave para su funcionamiento.

Para configurar un sistema RSA, se eligen dos números primos muy grandes, 'p' y 'q'. Luego se calcula 'n' = 'p' * 'q' y 'k' = φ(n). También se encuentran dos números 'e' y 'd' que cumplen una condición especial relacionada con 'k'.

Los números 'n' y 'e' (la "clave de cifrado") se hacen públicos. El número 'd' (la "clave de descifrado") se mantiene en secreto.

Cuando alguien quiere enviarte un mensaje (representado por un número 'm'), lo "cifra" usando 'n' y 'e'. Tú, con tu clave secreta 'd', puedes "descifrar" el mensaje. El Teorema de Euler garantiza que esto funciona.

La seguridad del sistema RSA se basa en que es muy difícil calcular φ(n) o encontrar los factores primos 'p' y 'q' de 'n' si 'n' es un número muy grande. Como solo tú conoces 'p' y 'q' (porque los elegiste al principio), nadie más puede descifrar tus mensajes fácilmente.

Problemas sin resolver

En matemáticas, siempre hay preguntas sin respuesta. Aquí hay algunas relacionadas con la función phi:

Conjetura de Lehmer

Si 'p' es un número primo, sabemos que φ(p) = p - 1. La conjetura de Lehmer pregunta si existe algún número 'n' que no sea primo, pero para el cual φ(n) divida a n - 1. Hasta ahora, no se ha encontrado ningún número así. Los matemáticos han demostrado que si existiera, sería un número enorme.

Conjetura de Carmichael

La conjetura de Carmichael dice que no hay ningún número 'n' para el cual φ(n) sea único. Es decir, para cualquier 'n', siempre habrá otro número 'm' diferente de 'n' tal que φ(m) = φ(n). Por ejemplo, φ(12) = 4 y φ(8) = 4. Si esta conjetura fuera falsa, el contraejemplo más pequeño sería un número con al menos diez mil millones de dígitos.

Ver también

• Teorema de Euler
• Número altamente totiente
• Número no totiente
• Número totiente perfecto
• Pequeño teorema de Fermat
• RSA

Véase también

En inglés: Euler's totient function Facts for Kids