Entropía (información) para niños
La entropía de la información, también conocida como entropía de Shannon, es una idea importante en la teoría de la información. Imagina que tienes un mensaje o una señal. La entropía mide qué tan "incierto" o "impredecible" es ese mensaje. También nos dice cuánta información nueva contiene en promedio.
Piensa en las palabras de un texto. Palabras muy comunes como "el" o "que" no nos dan mucha información si las vemos. Si borras un "que" de una frase, probablemente seguirás entendiendo el mensaje. Pero si borras una palabra menos común, como "perro", la frase podría perder su sentido. Esto es porque las palabras menos comunes aportan más información.
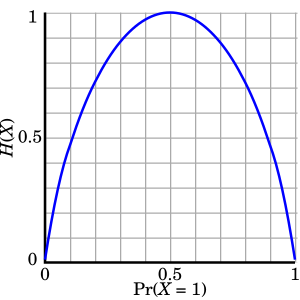
Cuando todos los posibles mensajes o símbolos son igual de probables, la entropía es máxima. Esto significa que no puedes predecir cuál será el siguiente, y cada uno te da mucha información nueva.
El concepto de entropía se usa en diferentes campos, como la termodinámica (que estudia el calor y la energía) y la seguridad entrópica (que se usa en la seguridad de la información). En todos estos casos, la entropía se relaciona con la incertidumbre y la cantidad de información que necesitamos para entender o reducir esa incertidumbre.
Contenido
- ¿Cómo se relaciona con la termodinámica?
- Entendiendo la entropía de la información
- ¿Cómo se calcula la entropía?
- Propiedades de la entropía
- Codificador óptimo: ¿Cómo comprimir información?
- Entropía condicional: ¿Qué pasa si sabemos algo?
- Entropía de un proceso estocástico
- Otros tipos de entropía
- Véase también
¿Cómo se relaciona con la termodinámica?
La entropía en la teoría de la información tiene una conexión con la entropía termodinámica. En termodinámica, la entropía se usa para describir el desorden o la aleatoriedad de un sistema, como un gas o un líquido. Cuanto más desordenado y disperso está un sistema, mayor es su entropía.
Por ejemplo, si tienes un gas en una esquina de una habitación, sus partículas están más ordenadas. Con el tiempo, esas partículas se dispersarán por toda la habitación, aumentando el desorden y, por lo tanto, la entropía. Esto se conoce como la segunda ley de la termodinámica, que dice que el desorden en un sistema aislado tiende a aumentar.
La entropía de la información es similar: mide el desorden o la imprevisibilidad de los mensajes. Si un mensaje es muy predecible, tiene poca entropía (poco desorden). Si es muy impredecible, tiene mucha entropía (mucho desorden).
Entendiendo la entropía de la información
La idea principal de la entropía en la teoría de la información tiene que ver con la incertidumbre en cualquier experimento o señal. También se puede ver como la cantidad de "ruido" o "desorden" que contiene un sistema. Así, podemos saber cuánta información lleva una señal.
Imagina un texto escrito en español. Está formado por letras, espacios y signos de puntuación. Algunas letras, como la "a", son muy comunes, mientras que otras, como la "w", no lo son tanto. Esto significa que el texto no es completamente "aleatorio". Aunque no podemos adivinar con exactitud cuál será el siguiente carácter, la entropía nos ayuda a medir qué tan aleatorio es. Esta idea fue presentada por Claude Shannon en 1948.
Shannon definió la entropía con dos ideas clave:
- La cantidad de información debe ser proporcional. Esto significa que si la probabilidad de que aparezca un elemento cambia un poco, la entropía también debería cambiar un poco.
- Si todos los elementos de una señal tienen la misma probabilidad de aparecer, entonces la entropía será la más alta posible. Esto tiene sentido, porque si todo es igual de probable, es más difícil adivinar qué vendrá después.
Ejemplos de máxima entropía
Piensa que estás esperando un mensaje por cable, y solo puede contener letras minúsculas de la "a" a la "z". Si el mensaje que recibes es "qalmnbphijcdgketrsfuvxyzwño", que tiene 27 caracteres, este mensaje tiene la máxima entropía posible. ¿Por qué? Porque los caracteres no se repiten y no siguen ningún orden predecible. Es muy difícil adivinar cuál será el siguiente carácter.
¿Cómo se calcula la entropía?
La entropía se calcula usando las probabilidades de que ocurran los diferentes eventos o símbolos. Si un evento es muy probable, aporta poca información. Si es poco probable, aporta mucha.
Por ejemplo, si tienes un mensaje con tres posibles estados (M1, M2, M3) y M1 tiene un 50% de probabilidad de aparecer, mientras que M2 y M3 tienen un 25% cada uno. M1 es más predecible, así que aporta menos información que M2 o M3. La entropía de este mensaje se calcularía sumando la información que aporta cada estado, considerando su probabilidad.
Propiedades de la entropía
La entropía tiene algunas características importantes:
- Siempre es positiva: La entropía siempre es un número igual o mayor que cero.
- Tiene un límite máximo: La entropía es más alta cuando todos los posibles resultados son igual de probables. Esto significa que hay la mayor incertidumbre sobre el mensaje.
- Es cero cuando no hay incertidumbre: Si un resultado es seguro (su probabilidad es 1, y los demás son 0), la entropía es cero. Esto significa que no hay ninguna incertidumbre sobre el mensaje que se recibirá.
Codificador óptimo: ¿Cómo comprimir información?
Un codificador óptimo es como un sistema inteligente que usa la menor cantidad de "bits" (la unidad básica de información en computadoras) para guardar o enviar un mensaje. Este codificador es muy eficiente: usa códigos cortos para los mensajes o símbolos que aparecen con más frecuencia, y códigos más largos para los que son menos comunes. Así, se aprovecha al máximo el espacio de almacenamiento o el canal de comunicación.
Un ejemplo famoso es el código Morse. Aunque no es perfecto, asigna códigos más cortos a las letras más usadas en inglés (como la "e" o la "t") y códigos más largos a las menos usadas (como la "q" o la "z").
Otro ejemplo es el algoritmo de Huffman, que se usa para comprimir archivos. Este algoritmo primero cuenta cuántas veces aparece cada carácter en un texto y luego crea un código óptimo para cada uno, usando árboles binarios.
La entropía nos dice cuál es el número promedio de bits que se necesitan para codificar un mensaje de la manera más eficiente posible, sin perder información. Es como el límite de compresión que se puede alcanzar.
Ejemplo de codificador óptimo
Imagina de nuevo nuestro mensaje con tres estados: M1 (50% de probabilidad), M2 (25%), y M3 (25%).
- Para M1, que es muy probable, solo necesitaríamos 1 bit (por ejemplo, "0").
- Para M2 y M3, que son menos probables, necesitaríamos 2 bits (por ejemplo, "10" para M2 y "11" para M3).
Si tuviéramos un mensaje como M1 M2 M1 M1 M3 M1 M2 M3, lo codificaríamos como "010001101011", usando 12 bits en total. En promedio, este sistema usa 1.5 bits por cada parte del mensaje, lo cual es muy eficiente.
Entropía condicional: ¿Qué pasa si sabemos algo?
A veces, la probabilidad de un evento depende de otro. La entropía condicional mide cómo la incertidumbre de un evento disminuye si ya conocemos el resultado de otro evento relacionado.
Por ejemplo, si sabes que está lloviendo (evento Y), la probabilidad de que necesites un paraguas (evento X) cambia. La entropía condicional nos diría cuánta incertidumbre sobre el paraguas se reduce al saber que llueve.
Aplicación en seguridad de la información
Este concepto es muy útil en el criptoanálisis, que es el estudio de cómo romper códigos secretos. Si un mensaje está cifrado, la entropía condicional puede ayudar a saber qué tan seguro es el cifrado.
Por ejemplo, si un atacante conoce una parte del mensaje cifrado, la entropía condicional puede decirles cuánta incertidumbre queda sobre la clave secreta o sobre el resto del mensaje original. Si la incertidumbre se reduce a cero, significa que el cifrado se ha roto.
Entropía de un proceso estocástico
Un proceso estocástico es una secuencia de eventos aleatorios que ocurren con el tiempo, como el clima día a día o los resultados de lanzar una moneda muchas veces. La entropía de un proceso estocástico mide la incertidumbre de toda la secuencia de eventos.
Por ejemplo, si analizamos una secuencia de letras en un idioma, algunas secuencias son más probables que otras (como "qu" en español). La entropía de esta secuencia nos diría qué tan predecible es el siguiente grupo de letras.
Tasa de entropía
La tasa de entropía nos dice cómo crece la incertidumbre de una secuencia de eventos a medida que la secuencia se hace más larga. Es como medir la cantidad de información nueva que se añade por cada nuevo evento en un proceso continuo.
Otros tipos de entropía
Además de la entropía de Shannon, existen otras formas de medir la información o la incertidumbre, que son útiles en diferentes situaciones. Algunas de ellas son:
- Entropía lineal
- Entropía de Rényi
- Entropía de tsallis
Todas estas medidas tienen en común que son mayores o iguales a cero, y alcanzan su valor máximo cuando todos los resultados posibles son igual de probables.
Véase también
 En inglés: Information entropy Facts for Kids
En inglés: Information entropy Facts for Kids
- Seguridad entrópica
- Entropía cruzada
- Perplejidad
- Capacidad de canal
- Neguentropía o Sintropía (lo opuesto a la entropía, representa el orden)