Distribución de Gumbel para niños
Datos para niños Distribución de Gumbel |
||
|---|---|---|
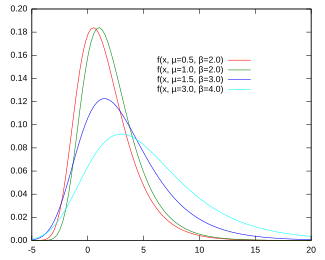 Función de densidad de probabilidad |
||
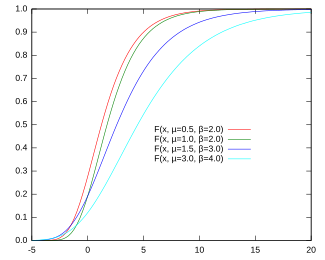 Función de distribución de probabilidad |
||
| Parámetros | 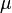 location (real) location (real) scale (real) scale (real) |
|
| Dominio | 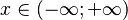 |
|
| Función de densidad (pdf) |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{z\,e^{-z</td></tr><tr><td class="noprint" colspan="3" style="text-align:left;"></td></tr></table><!--IB_END-->{\beta}\! En el mundo de la teoría de probabilidad y la estadística, la distribución de Gumbel es una herramienta muy útil. Fue nombrada así por Emil Julius Gumbel, un matemático que vivió entre 1891 y 1966. Esta distribución se usa para entender y predecir eventos extremos. Imagina que quieres saber cuál podría ser el nivel más alto que alcanzará un río en los próximos años, basándote en los datos de los niveles máximos de los últimos 10 años. La distribución de Gumbel te ayuda a modelar estos "valores extremos", ya sean los más altos o los más bajos. Es muy útil para predecir fenómenos naturales como inundaciones o sequías. La razón por la que la distribución de Gumbel funciona tan bien para los valores máximos es que se basa en la teoría de valores extremos. Esta teoría dice que si tus datos siguen una distribución normal o distribución exponencial, la distribución de Gumbel será muy útil para analizar los valores más grandes o más pequeños. Contenido
¿Qué características tiene la distribución de Gumbel?La distribución de Gumbel tiene varias características importantes que la describen. Estas propiedades nos ayudan a entender cómo se comportan los datos que modela. ¿Cómo se calcula la probabilidad acumulada?La función de distribución acumulada (FDC) de Gumbel nos dice la probabilidad de que un valor sea menor o igual a un cierto número. Es como saber la probabilidad de que el nivel del río no supere una altura específica. ¿Cuál es el valor central de los datos?En estadística, usamos la media, la mediana y la moda para describir el centro de un conjunto de datos.
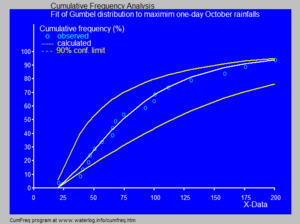
Para la distribución de Gumbel, la moda es el parámetro μ (mu), que es un valor clave en su definición. ¿Qué tan dispersos están los datos?La desviación estándar nos indica qué tan dispersos están los datos alrededor de la media. Una desviación estándar pequeña significa que los datos están muy juntos, mientras que una grande indica que están muy separados. ¿Qué es la distribución estándar de Gumbel?La distribución estándar de Gumbel es un caso especial y más simple. Ocurre cuando los parámetros μ (mu) y β (beta) tienen valores específicos: μ es 0 y β es 1. En este caso, las fórmulas se simplifican, pero sigue siendo muy útil para entender el comportamiento básico de la distribución. ¿Cómo se usan los datos para estimar los parámetros?Para usar la distribución de Gumbel en la vida real, necesitamos estimar sus parámetros (μ y β) a partir de los datos que tenemos. Una forma práctica es usar la mediana de nuestros datos. Luego, ajustamos el valor de μ hasta que la distribución se adapte bien a nuestro conjunto de valores. Esto nos permite crear un modelo que represente nuestros datos. ¿Cómo se generan variables de Gumbel?A veces, los científicos y matemáticos necesitan crear números aleatorios que sigan una distribución de Gumbel. Esto es útil para simulaciones o para probar modelos. Se puede hacer tomando un número aleatorio de una distribución uniforme (donde todos los números tienen la misma probabilidad de aparecer) y luego aplicando una fórmula especial. El resultado será un número que sigue la distribución de Gumbel. ¿Qué otras distribuciones están relacionadas?La distribución de Gumbel tiene "parientes" en el mundo de la estadística. Por ejemplo, la Distribución de Gompertz está relacionada con la distribución de Gumbel estándar. Esto significa que si conoces una, puedes entender la otra. ¿Existe una versión opuesta de la distribución de Gumbel?Sí, algunos expertos usan una versión ligeramente diferente llamada la distribución de Gumbel opuesta. Esta versión se utiliza para modelar valores mínimos en lugar de máximos. Por ejemplo, podría usarse para predecir la temperatura más baja en un lugar durante un período de tiempo. ¿Para qué se aplica la distribución de Gumbel?La distribución de Gumbel es muy importante en varias áreas: Hidrología y eventos naturalesEn la hidrología (el estudio del agua), la distribución de Gumbel se usa mucho. Ayuda a analizar datos como los niveles máximos de lluvia o el caudal de los ríos. También es útil para describir períodos de sequía, que son los valores mínimos de lluvia. Gumbel demostró que esta distribución es muy precisa para predecir los valores más altos en muestras grandes de datos. Análisis de frecuencia de datosCuando tenemos una serie de datos y queremos entender la frecuencia con la que ocurren ciertos valores, la distribución de Gumbel es una herramienta clave. Por ejemplo, si ordenamos los datos de lluvia máxima de un año, podemos usar esta distribución para estimar la probabilidad de que ocurra una lluvia de cierta intensidad. La imagen azul muestra cómo se ajusta la distribución de Gumbel a los datos de lluvias máximas diarias, ayudando a los científicos a entender y predecir estos eventos. ¿Qué herramientas de software se usan?Para trabajar con la distribución de Gumbel y ajustar modelos a los datos, los expertos usan programas de computadora especiales. Estos programas pueden calcular los parámetros y mostrar cómo se ajusta la distribución a los datos reales. Algunos ejemplos de software incluyen herramientas como MathWorks, Ricci distributions, Risksolver y CumFreq. Véase también
|
|


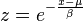 | cdf =
| cdf =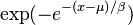 | media =
| media =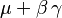 | mediana =
| mediana =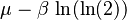 | moda =
| moda =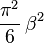 | simetría =
| simetría =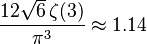 | curtosis =
| curtosis =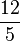 | =
| = | mgf =
| mgf =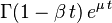 | car =
| car =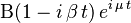 }}
}}
 En inglés:
En inglés: