Distancia euclidiana para niños
En matemáticas, la distancia euclidiana es la forma más común de medir la distancia entre dos puntos. Imagina que es como usar una regla para medir en línea recta. Esta idea se basa en el famoso teorema de Pitágoras.
Por ejemplo, en un plano (un espacio de dos dimensiones), la distancia euclidiana entre dos puntos P1 y P2 se calcula usando sus coordenadas cartesianas. Si P1 está en (x1, y1) y P2 está en (x2, y2), la distancia es:
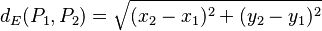
Contenido
Distancia Euclidiana: Midiendo en Línea Recta
La distancia euclidiana es la medida "normal" que usamos en nuestra vida diaria. Es la distancia más corta entre dos puntos, como si trazaras una línea recta entre ellos. Se llama "euclidiana" por el matemático griego Euclides, quien sentó las bases de la geometría que usamos hoy.
¿Qué es la Distancia Euclidiana?
Piensa en un mapa o en un plano de tu casa. Si quieres saber qué tan lejos está un lugar de otro, la distancia euclidiana es la que medirías con una cinta métrica en línea recta. No es la distancia que recorrerías siguiendo calles o pasillos, sino la distancia directa.
¿Cómo se Calcula? El Teorema de Pitágoras al Rescate
La clave para entender la distancia euclidiana es el teorema de Pitágoras. Este teorema dice que en un triángulo rectángulo (uno que tiene un ángulo de 90 grados), el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados.
Distancia en un Plano (2D)
Imagina que tienes dos puntos en un plano, como en una hoja de papel cuadriculado. Llamemos a estos puntos P y Q.
- P tiene coordenadas (x1, y1).
- Q tiene coordenadas (x2, y2).
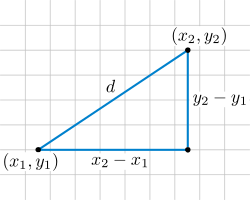
Para encontrar la distancia entre P y Q, podemos formar un triángulo rectángulo.
- La diferencia en las coordenadas 'x' (x2 - x1) es un lado del triángulo.
- La diferencia en las coordenadas 'y' (y2 - y1) es el otro lado.
- La distancia entre P y Q es la hipotenusa.
Aplicando el teorema de Pitágoras, la distancia (d) es la raíz cuadrada de la suma de los cuadrados de esas diferencias: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}
Distancia en el Espacio (3D y más)
Si los puntos están en un espacio de tres dimensiones (como una habitación, donde también hay altura), solo necesitamos añadir una coordenada más: 'z'.
- P tiene coordenadas (p1, p2, p3).
- Q tiene coordenadas (q1, q2, q3).
La fórmula se extiende de manera similar: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d_E(P,Q)=\sqrt{(p_1-q_1)^2 + (p_2-q_2)^2 + (p_3-q_3)^2}
Y si tuviéramos más dimensiones (aunque es difícil de imaginar), la idea es la misma: sumamos el cuadrado de la diferencia de cada coordenada y luego sacamos la raíz cuadrada de todo.
Véase también
 En inglés: Euclidean distance Facts for Kids
En inglés: Euclidean distance Facts for Kids