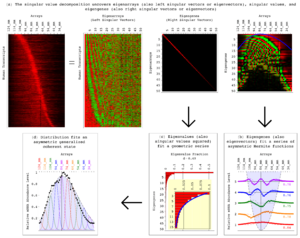
Descomposición en valores singulares para niños
La descomposición en valores singulares (o DVS) es una herramienta matemática muy útil en el álgebra lineal. Imagina que tienes una tabla grande de números, llamada matriz. La DVS es una forma especial de "romper" o "factorizar" esa tabla en tres partes más sencillas. Esto ayuda a entender mejor la información que contiene la tabla y se usa mucho en áreas como la estadística y la ciencia de datos.
Contenido
¿Qué es la Descomposición en Valores Singulares?
La DVS es como una receta para desarmar una matriz (una tabla de números) en tres matrices más simples. Piensa en una matriz como una transformación que cambia vectores (flechas con dirección y longitud). La DVS nos dice cómo esa transformación estira, encoge o rota los vectores.
La fórmula general de la DVS para una matriz A es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = U \Sigma V^t
Aquí, cada letra representa una matriz especial:
- A es la matriz original que queremos descomponer.
- U es una matriz que representa las rotaciones o giros en el espacio de salida.
- Σ (Sigma) es una matriz diagonal que contiene los "valores singulares". Estos valores nos dicen cuánto se estira o encoge la información en ciertas direcciones. Son siempre números positivos o cero y se ordenan de mayor a menor.
- V es una matriz que representa las rotaciones o giros en el espacio de entrada. La t en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V^t significa que la matriz está "transpuesta", es decir, sus filas y columnas se intercambian.
¿Qué son los Valores Singulares?
Los valores singulares son números que nos indican la "importancia" o "fuerza" de ciertas direcciones en los datos de la matriz. Cuanto mayor sea un valor singular, más importante es la dirección asociada a él. Estos valores se calculan a partir de los valores propios de una matriz relacionada con la original.
Por ejemplo, si tienes una matriz que representa una imagen, los valores singulares más grandes podrían corresponder a las características más importantes de la imagen, como los bordes principales o las formas grandes.
¿Cómo se calcula la DVS?
El cálculo de la DVS implica encontrar los valores propios y vectores propios de matrices especiales que se forman a partir de la matriz original. Aunque el proceso matemático es complejo, la idea principal es identificar las direcciones en las que la matriz "estira" o "encoge" los datos de la manera más significativa.
- Primero, se calculan los valores propios de la matriz Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A^tA (la matriz original multiplicada por su transpuesta). Estos valores propios son siempre positivos o cero.
- Luego, se saca la raíz cuadrada de esos valores propios para obtener los valores singulares.
- Finalmente, se construyen las matrices U, Σ y V usando estos valores singulares y los vectores propios asociados.
Descomposición en Valores Singulares Reducida
A veces, no necesitamos toda la información de la DVS, especialmente si la matriz original es muy grande. La DVS reducida es una versión más compacta que se queda solo con los valores singulares que no son cero y sus vectores asociados. Esto es útil para ahorrar espacio y tiempo de cálculo, y a menudo es suficiente para muchas aplicaciones.
¿Para qué se usa la DVS?
La DVS tiene muchas aplicaciones prácticas en el mundo real. Aquí te mostramos algunas:
Compresión de Datos
La DVS puede usarse para reducir el tamaño de los datos sin perder demasiada información importante. Por ejemplo, en la compresión de imágenes, se pueden guardar solo los valores singulares más grandes y reconstruir una imagen muy parecida a la original, pero con menos datos.
Reducción de Ruido
En señales o imágenes con ruido (información no deseada), la DVS puede ayudar a eliminar ese ruido. Al quedarse con los valores singulares más grandes, se filtra la información principal y se descarta el ruido, que suele estar asociado a valores singulares pequeños.
Sistemas de Recomendación
¿Alguna vez te has preguntado cómo Netflix o Spotify te recomiendan películas o canciones? La DVS es una de las técnicas que se usan para analizar tus preferencias y las de otros usuarios, y así predecir qué te podría gustar.
Búsqueda de Información
En la búsqueda de documentos o textos, la DVS puede ayudar a encontrar documentos que son similares en su contenido, incluso si no usan exactamente las mismas palabras. Esto se conoce como indexación semántica latente.
Resolución de Problemas Matemáticos
La DVS es una herramienta fundamental para resolver ciertos tipos de ecuaciones matemáticas, especialmente cuando las matrices involucradas no son cuadradas o no tienen una "inversa" normal.
- Pseudoinversa: La DVS permite calcular la "pseudoinversa" de una matriz, que es como una inversa para matrices que no tienen una inversa tradicional. Esto es útil para encontrar las mejores soluciones aproximadas a sistemas de ecuaciones.
- Solución de Ecuaciones: Ayuda a encontrar soluciones para sistemas de ecuaciones lineales, incluso cuando hay muchas soluciones posibles o ninguna solución exacta.
Ejemplos Sencillos de DVS
Aunque el cálculo completo es complejo, podemos ver cómo se aplica la idea.
Ejemplo 1
Imagina una matriz simple Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \begin{pmatrix} 0 & 0 \\ 0 & 9 \\ 3 & 0 \end{pmatrix} . Al aplicar la DVS, encontramos que sus valores singulares son 9 y 3. Esto significa que hay dos direcciones principales en las que esta matriz "estira" los datos, una 9 veces y otra 3 veces. La DVS nos permite reescribir esta matriz como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 9 & 0 \\ 0 & 3 \\ 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} Esta es la misma matriz A, pero expresada como el producto de tres matrices más simples.
Ejemplo 2
Considera otra matriz Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): B = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 1 \end{pmatrix} . Para esta matriz, el único valor singular no nulo es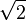 
(aproximadamente 1.414). Esto nos dice que solo hay una dirección principal en la que esta matriz tiene un efecto significativo. La DVS de esta matriz sería: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): B = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} \sqrt{2} & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} De nuevo, la matriz original se descompone en tres partes que revelan sus propiedades de estiramiento y rotación.
Galería de imágenes
-
Una imagen que explica brevemente el tema
Véase también
En inglés: Singular value decomposition Facts for Kids
