Derivada de segundo orden para niños

En el cálculo, la segunda derivada de una función es como la "derivada de la derivada". Imagina que la primera derivada te dice qué tan rápido cambia algo. Pues la segunda derivada te dice qué tan rápido cambia esa velocidad.

Por ejemplo, si estás en un coche, la primera derivada de tu posición te da tu velocidad. La segunda derivada de tu posición te da la aceleración, que es qué tan rápido cambia tu velocidad. Si aceleras, tu velocidad aumenta; si frenas, tu velocidad disminuye. La segunda derivada mide ese cambio.

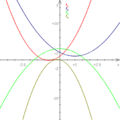
En el gráfico de una función, la segunda derivada nos ayuda a entender la forma de la curva. Nos dice si la curva se abre hacia arriba (como una U) o hacia abajo (como una U invertida).

La segunda derivada de una función cuadrática es constante.

¿Cómo se calcula la segunda derivada?

Calcular la segunda derivada es como hacer el mismo paso dos veces. Primero, calculas la derivada de la función original. Luego, tomas el resultado de esa primera derivada y le calculas la derivada otra vez.

Regla de la potencia para la segunda derivada

Si tienes una función como x elevado a una potencia (por ejemplo, x³ o x⁵), puedes usar una regla sencilla. Para la primera derivada, bajas la potencia y le restas uno al exponente. Para la segunda derivada, haces eso dos veces:

• Si tienes x elevado a n (xⁿ), la primera derivada es n multiplicado por x elevado a n menos 1 (nxⁿ⁻¹).
• La segunda derivada es n multiplicado por (n menos 1) multiplicado por x elevado a n menos 2 (n(n-1)xⁿ⁻²).

Por ejemplo, si tienes f(x) = x³,

• La primera derivada es f'(x) = 3x² (bajas el 3 y le restas 1 al exponente).
• La segunda derivada es f(x) = 6x (bajas el 2 del 3x² y lo multiplicas por 3, y le restas 1 al exponente).

Notación de la segunda derivada

Para no escribir "la segunda derivada de f(x)" todo el tiempo, usamos símbolos especiales:

• La forma más común es poner dos comillas después de la letra de la función, así: f(x). Esto significa que es la derivada de la primera derivada (f')'.
• Otra forma, usada en notación de Leibniz, es escribir Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{d^2y}{dx^2} . Esto significa que derivamos y dos veces con respecto a x.

¿Qué nos dice la segunda derivada sobre la gráfica?

La segunda derivada nos da información clave sobre la forma de la gráfica de una función.

Concavidad de la gráfica

La segunda derivada nos indica la concavidad de la gráfica:

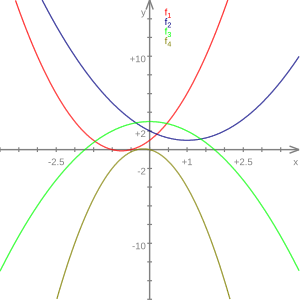
• Si la segunda derivada es positiva (f(x) > 0), la gráfica es cóncava hacia arriba. Imagina una sonrisa o una taza que puede contener agua. Las líneas tangentes a la curva estarán por debajo de ella.
• Si la segunda derivada es negativa (f(x) < 0), la gráfica es cóncava hacia abajo. Imagina una cara triste o una montaña. Las líneas tangentes a la curva estarán por encima de ella.

Una gráfica de . La línea tangente es azul donde la curva es cóncava hacia arriba, verde donde es cóncava hacia abajo y roja en los puntos de inflexión.

Puntos de inflexión

Un punto de inflexión es un lugar en la gráfica donde la concavidad cambia. Es decir, la curva pasa de ser cóncava hacia arriba a cóncava hacia abajo, o al revés. En estos puntos, la segunda derivada suele ser cero. Sin embargo, no todos los puntos donde la segunda derivada es cero son puntos de inflexión.

Prueba de la segunda derivada

La segunda derivada también nos ayuda a encontrar los puntos más altos (máximos) o más bajos (mínimos) de una función. Estos puntos se llaman "puntos estacionarios" porque la primera derivada es cero allí (la función no está subiendo ni bajando en ese instante).

• Si en un punto estacionario la segunda derivada es negativa (f(x) < 0), entonces tienes un máximo local (un "pico" en la gráfica).
• Si en un punto estacionario la segunda derivada es positiva (f(x) > 0), entonces tienes un mínimo local (un "valle" en la gráfica).
• Si la segunda derivada es cero (f(x) = 0), esta prueba no nos dice si es un máximo, un mínimo o un punto de inflexión. Necesitaríamos otras pruebas.

Piensa en un coche:

• Si tu velocidad es cero (punto estacionario) y tu aceleración es negativa (frenas), significa que estabas yendo hacia adelante y te detuviste en tu punto más lejano, un máximo.
• Si tu velocidad es cero y tu aceleración es positiva (aceleras), significa que estabas yendo hacia atrás y te detuviste en tu punto más cercano, un mínimo.

Galería de imágenes

• 

  La derivada de segundo orden de una función cuadrática es constante.

• 

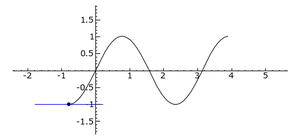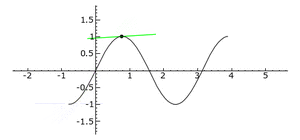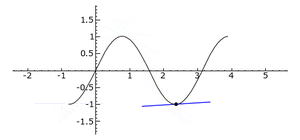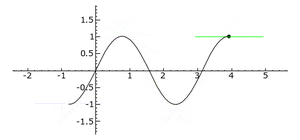
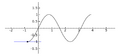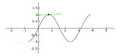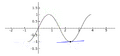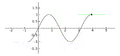
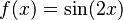  Una gráfica de . La línea tangente es azul donde la curva es cóncava hacia arriba, verde donde es cóncava hacia abajo y roja en los puntos de inflexión.