Sistema trifásico para niños

Enciclopedia para niños

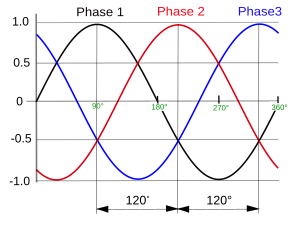
En ingeniería eléctrica, un sistema trifásico es un sistema de producción, distribución y consumo de energía eléctrica formado por tres corrientes alternas monofásicas de igual frecuencia y amplitud (y por consiguiente valor eficaz), que presentan una diferencia de fase entre ellas de 120° eléctricos, y están dadas en un orden determinado. Cada una de las corrientes monofásicas que forman el sistema se designa con el nombre de fase.

Tensión en las fases de un sistema trifásico equilibrado. Entre cada una de las fases hay un desfase de 120°.

Un sistema trifásico de tensiones se dice que es equilibrado cuando sus corrientes tienen magnitudes iguales y están desfasadas simétricamente.

Cuando alguna de las condiciones anteriores no se cumple (corrientes diferentes o distintos desfases entre ellas), el sistema de tensiones está desequilibrado o más comúnmente llamado un sistema desbalanceado. Recibe el nombre de sistema de cargas desequilibradas, el conjunto de impedancias distintas que dan lugar a que por el receptor circulen corrientes de amplitudes diferentes o con diferencias de fase entre ellas distintas a 120°, aunque las tensiones del sistema o de la línea sean equilibradas o balanceadas.

El sistema trifásico presenta una serie de ventajas, como son la economía de sus líneas de transporte de energía (hilos de menor sección que en una línea monofásica equivalente) y de los transformadores utilizados, así como su elevado rendimiento de los receptores, especialmente motores, a los que la línea trifásica alimenta con potencia constante.

Los generadores utilizados en centrales eléctricas son trifásicos, dado que la conexión a la red eléctrica debe ser trifásica (salvo para centrales de poca potencia). La trifásica se usa masivamente en industrias, donde las máquinas funcionan con motores trifásicos.

Existen dos tipos principales de conexión; en triángulo y en estrella. En estrella, el neutro es el punto de unión de las fases.

Contenido

Conexión en estrella (del generador o de la carga)
Conexión en triángulo (del generador o de la carga)
Potencia en los sistemas trifásicos equilibrados
Compensación de potencia
Disposición de la bornera o placa de conexiones
Transferencia constante de potencia con cargas equilibradas
Cableado
Véase también

Conexión en estrella (del generador o de la carga)

En un generador en configuración estrella, las intensidades de fase coinciden con las correspondientes de línea, por lo que se cumple (en caso de equilibrio) $I_F = I_L$ .

Las tensiones de fase y de línea en configuración estrella (en caso de equilibrio) se relacionan por 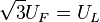$\sqrt{3} U_F = U_L$ , relación obtenida al aplicar la segunda ley de Kirchhoff a los fasores 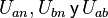$U_{an}, U_{bn}\, \textsf{y}\, U_{ab}$ de modo que resulta (transformando los fasores en vectores (x,y) para facilitar el cálculo): 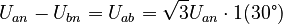$U_{an}-U_{bn}=U_{ab}=\sqrt{3} U_{an}\cdot 1(30\text{°})$ siendo 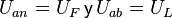$U_{an}=U_F\, \textsf{y}\, U_{ab}=U_L$ . Esta relación es visualizable dibujando el diagrama de estos fasores de tensión.

Conexión en triángulo (del generador o de la carga)

Si se conectan entre sí las fases del generador o de la carga, conectando el principio de cada fase con el final de la siguiente, se obtiene la configuración triángulo.

En configuración triángulo, la intensidad de fase y la intensidad de línea se relacionan por 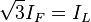$\sqrt{3} I_F=I_L$ , relación obtenida al aplicar la primera ley de Kirchhoff a los fasores de intensidad de cualquiera de los tres nodos de modo que resulta .... 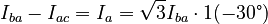$I_{ba}-I_{ac}=I_a=\sqrt{3} I_{ba}\cdot 1(-30\text{°})$ siendo $I_a=I_L$ . Esta relación es visualizable dibujando el diagrama de estos fasores de intensidad.

Las tensiones de fase y de línea en configuración triángulo coinciden $U_F=U_L$ , lo que es evidente porque cada rama de fase conecta dos líneas entre sí.

Potencia en los sistemas trifásicos equilibrados

Triángulo de Potencias

La potencia suministrada por un generador trifásico o la consumida por un receptor trifásico, es la suma de las potencias suministradas o consumidas por cada fase.

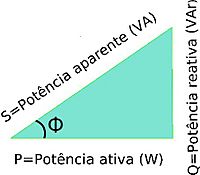
Por lo tanto, la potencia aparente será 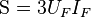$\text{S} = 3U_FI_F$ ; la potencia activa, 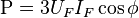$\text{P}=3U_FI_F \cos\phi$ ; y la potencia reactiva,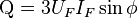 $\text{Q}=3U_FI_F\sin\phi$

Relacionando los valores de fase con los valores de línea, tendremos

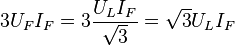$3U_FI_F = 3\frac{U_LI_F}\sqrt{3} = \sqrt{3}U_LI_F$ ,

que corresponde a la potencia aparente de un sistema trifásico. Teniendo en cuenta los desfasajes para cargas inductivas o capacitivas, obtenemos;

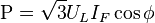$\text{P}= \sqrt{3}U_LI_F\cos\phi$ para la potencia activa, y

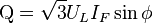$\text{Q}= \sqrt{3}U_LI_F\sin\phi$ para la potencia reactiva.

Compensación de potencia

Dado el coste económico que supone la potencia reactiva para una central eléctrica, se tiende a eliminarla ("compensarla") añadiendo condensadores o bobinas a la carga.

Para deducir la fórmula directa del valor de, por ejemplo, los condensadores hay que partir de saber cuánta potencia reactiva Q se quiere compensar. Los condensadores se colocarán inicialmente en paralelo a la carga (en estrella), por tanto su U será igual a la de fase en la carga. Toda la potencia de un condensador es reactiva Q = I*U. Sabiendo que la admitancia compleja del condensador Y = jωC, que Z = 1/Y y que por la ley de Ohm U = I*Z = I*(-1/ωC) = I/(-ωC) (cuidado con la inversa de un número complejo) se obtiene que para un condensador Q = I*U = -ωC*U². Dado que no siempre se tiene Q sino la potencia activa P y el factor de potencia o el ángulo φ, la ecuación se suele escribir en función de la potencia activa de fase P_F y del ángulo φ de forma el condensador aporte la variación ΔQ que se pretende en el circuito (siendo por definición tgφ = Q/P y U = U_F = U de fase en la carga) ΔQ = Q₂ - Q₁ = (tgφ₂ - tgφ₁)*P_F = -ωC*U_F².

Disposición de la bornera o placa de conexiones

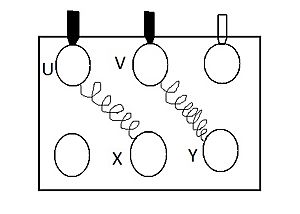
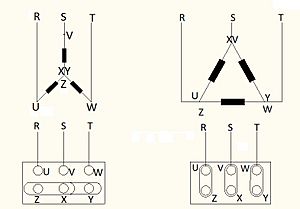
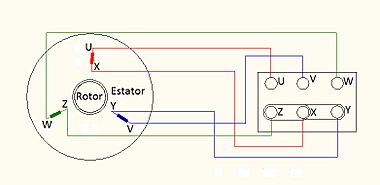
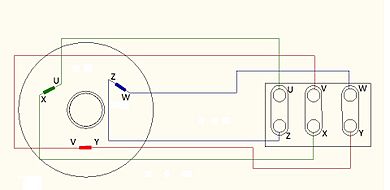
Para permitir una rápida y segura conexión a la red de las máquinas trifásica de C.A. los extremos de sus arrollamientos convergen a una bornera o placa de conexión ubicada sobre la carcasa exterior de dicha máquina. Lo bornes de dicha placa llevan la marca correspondiente a los principios U-V-W y finales X-Y-Z de los arrollamientos de la bornera pudiéndose pasar fácilmente de una conexión a otra con solo modificarse la posición de los puentes de conexión de los bornes.

Distribución interna de los bobinados de una bornera de una máquina trifásica

En la izquierda del lector se observa una conexión Estrella, en donde se unen todos los finales de bobina (X,Y,Z) y se obtiene el neutro. En la derecha se observa una conexión Triángulo, en donde se unen todos los "principios de bobina" (U,V,W) con los finales de bobina (Z,X,Y) respectivamente.

La razón por la cual se ha adoptado internacionalmente la disposición indicada en la bornera es que ambas conexiones se logran sin cruce de los puentes de conexión. Así entonces para la conexión estrella se unen con puentes horizontales los tres bornes superiores o los tres inferiores (indistintamente) mientras que para la conexión triángulo los puentes de conexión se ubican verticalmente.

Para facilitar el cambio de una conexión a otra, es usual contar en las borneras con la misma distancia entre bornes verticales y horizontales, lo que permite utilizar puentes de la misma longitud para una u otra conexión.

Esquema de interconexión entre bobinas de un alternador trifásico (ubicadas en el estátor) y la bornera en conexión Estrella alimentando a una línea de distribución de 4 conductores, tres de línea y un neutro.

Esquema de interconexión entre las bobinas del alternador trifásico (ubicadas en el estátor) y la bornera en conexión "Triángulo" alimentando a una línea de distribución de tres conductores.

Transferencia constante de potencia con cargas equilibradas

Considérese un sistema trifásico de tensiones:

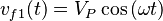
$v_{f1}(t)=V_P\cos\left(\omega t\right)\,\!$

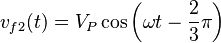
$v_{f2}(t)=V_P\cos\left(\omega t-\frac{2}{3}\pi\right)\,\!$

$v_{f3}(t)=V_P\cos\left(\omega t-\frac{4}{3}\pi\right)\,\!$

Si se asume la carga balanceada. Así, en cada fase hay impedancia:

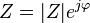
$Z=|Z|e^{j\varphi}\,$

con una corriente de pico

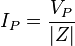
$I_P=\frac{V_P}{|Z|}$

y corrientes instantáneas

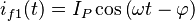
$i_{f1}(t)=I_P\cos\left(\omega t-\varphi\right)$

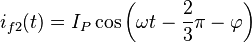
$i_{f2}(t)=I_P\cos\left(\omega t-\frac{2}{3}\pi-\varphi\right)$

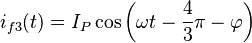
$i_{f3}(t)=I_P\cos\left(\omega t-\frac{4}{3}\pi-\varphi\right)$

Las potencias instantáneas en las fases son

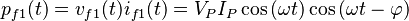
$p_{f1}(t)=v_{f1}(t)i_{f1}(t)=V_P I_P\cos\left(\omega t\right)\cos\left(\omega t-\varphi\right)$

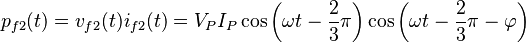
$p_{f2}(t)=v_{f2}(t)i_{f2}(t)=V_P I_P\cos\left(\omega t-\frac{2}{3}\pi\right)\cos\left(\omega t-\frac{2}{3}\pi-\varphi\right)$

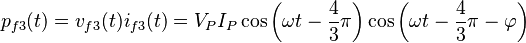
$p_{f3}(t)=v_{f3}(t)i_{f3}(t)=V_P I_P\cos\left(\omega t-\frac{4}{3}\pi\right)\cos\left(\omega t-\frac{4}{3}\pi-\varphi\right)$

Usando identidades trigonométricas:

$p_{f1}(t)=\frac{V_P I_P}{2}\left[\cos\varphi+\cos\left(2\omega t-\varphi\right)\right]$

$p_{f2}(t)=\frac{V_P I_P}{2}\left[\cos\varphi+\cos\left(2\omega t-\frac{4}{3}\pi-\varphi\right)\right]$

$p_{f3}(t)=\frac{V_P I_P}{2}\left[\cos\varphi+\cos\left(2\omega t-\frac{8}{3}\pi-\varphi\right)\right]$

que se suman para producir la potencia instantánea total

$p_{TOT}(t)=\frac{V_P I_P}{2}\left\{3\cos\varphi+\left[\cos\left(2\omega t-\varphi\right)+\cos\left(2\omega t-\frac{4}{3}\pi-\varphi\right)+\cos\left(2\omega t-\frac{8}{3}\pi-\varphi\right)\right]\right\}$

Como los términos en corchetes constituyen un sistema trifásico simétrico, ellos suman cero y la potencia total resulta constante

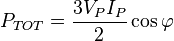
$P_{TOT}=\frac{3V_P I_P}{2}\cos\varphi$

o, sustituyendo la corriente de pico,

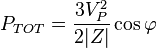
$P_{TOT}=\frac{3V_P^2}{2|Z|}\cos\varphi$

Cableado

Véase también: IEC 60446

La corriente trifásica es un sistema de tres corrientes alternas acopladas (las 3 corrientes se producen simultáneamente en un mismo generador). Cada una de estas corrientes (fases) se transporta por un conductor de fase (3 cables: R, S y T, con colores marrón, negro y gris), y se añade un conductor para el retorno común de las tres fases, que sirve para cerrar los 3 circuitos (conductor neutro N, color azul).

Véase también

En inglés: Three-phase electric power Facts for Kids

Corriente alterna
Instalación eléctrica
Sistema monofásico
Sistema polifásico
Sistema de suministro eléctrico
Transformación estrella-triángulo

Obtenido de «https://ninos.kiddle.co/index.php?title=Sistema_trifásico&oldid=3880522»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Sistema trifásico para Niños. Enciclopedia Kiddle.