Correlación para niños
En el mundo de la probabilidad y la estadística, la correlación nos ayuda a entender qué tan fuerte y en qué dirección se relacionan dos cosas o "variables". Imagina que tienes dos grupos de datos, como la cantidad de helados que se venden (variable A) y la temperatura del día (variable B). Si cuando la temperatura sube, también sube la venta de helados, decimos que hay una correlación entre ellas.
La correlación es muy útil porque nos puede dar pistas sobre cómo una cosa podría predecir otra. Por ejemplo, una compañía eléctrica podría saber que en días muy calurosos la gente usa más aire acondicionado. Basándose en esta correlación, pueden prepararse para producir más electricidad.
Es importante recordar que si dos cosas están correlacionadas, no significa que una cause la otra. Por ejemplo, la venta de helados y los ataques de tiburones pueden aumentar en verano, pero los helados no causan los ataques de tiburones. Ambos están relacionados con el calor del verano. Esto se llama "correlación no implica causalidad".
Existen diferentes formas de medir la correlación. Una de las más comunes es el coeficiente de correlación de Pearson. Este número nos dice qué tan fuerte es una relación lineal (como una línea recta) entre dos variables. Otros métodos, como la correlación de rangos de Spearman, son mejores para relaciones que no son tan rectas.
Contenido
¿Qué es el Coeficiente de Correlación de Pearson?
El Coeficiente de correlación de Pearson es la forma más conocida de medir cómo se relacionan dos grupos de números. Fue desarrollado por Karl Pearson basándose en ideas de Francis Galton.
Imagina que tienes muchos puntos en un gráfico, donde cada punto representa un par de datos (por ejemplo, la altura de una persona y su peso). El coeficiente de Pearson intenta encontrar la mejor línea recta que pase por esos puntos. El número que obtenemos nos dice qué tan cerca están los puntos de esa línea recta.
- Si el coeficiente es positivo (cerca de +1), significa que cuando una variable aumenta, la otra también tiende a aumentar. Es una relación directa.
- Si el coeficiente es negativo (cerca de -1), significa que cuando una variable aumenta, la otra tiende a disminuir. Es una relación inversa.
- Si el coeficiente es cero (o cerca de cero), significa que no hay una relación lineal clara entre las variables.
¿Cómo se relaciona la correlación con la independencia?
El valor del coeficiente de correlación de Pearson siempre está entre -1 y +1.
- Un valor de +1 significa una relación lineal directa perfecta.
- Un valor de -1 significa una relación lineal inversa perfecta.
- Un valor de 0 significa que no hay una relación lineal.
Si dos variables son completamente independientes (es decir, no tienen nada que ver una con la otra), su coeficiente de correlación de Pearson será 0. Sin embargo, si el coeficiente es 0, no siempre significa que las variables sean independientes. Podría haber una relación, pero no es una relación lineal (como una curva, por ejemplo).
¿Cómo se ve la correlación en un gráfico?
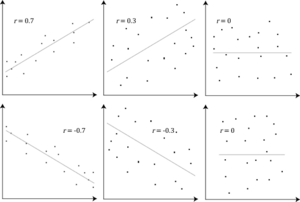
Cuando representamos cada par de datos como un punto en un gráfico, obtenemos lo que se llama una nube de puntos o diagrama de dispersión. La forma de esta nube de puntos nos ayuda a entender la correlación:
- Fuerza: Nos dice qué tan cerca están los puntos de formar una línea recta. Si los puntos están muy juntos y forman una línea delgada, la relación es fuerte. Si los puntos están muy dispersos, la relación es débil.
- Sentido: Nos indica la dirección de la relación. Si los puntos van hacia arriba de izquierda a derecha, la relación es directa (positiva). Si van hacia abajo, la relación es inversa (negativa).
- Forma: Nos dice si la relación es una línea recta, una curva suave o algo más complejo.
Tipos de Coeficientes de Correlación
Además del Coeficiente de correlación de Pearson, existen otros coeficientes para medir la correlación, dependiendo del tipo de datos que tengamos:
- Coeficiente de correlación de Spearman
- Correlación canónica
¿Cómo se entiende la correlación de forma geométrica?
Imagina que tus datos son como flechas (vectores) en un espacio. El coeficiente de correlación de Pearson es como el coseno del ángulo entre esas flechas.
- Si el coeficiente es 1, el ángulo es 0 grados, lo que significa que las flechas apuntan en la misma dirección.
- Si el coeficiente es 0, el ángulo es 90 grados, lo que significa que las flechas son perpendiculares (no se relacionan linealmente).
- Si el coeficiente es -1, el ángulo es 180 grados, lo que significa que las flechas apuntan en direcciones opuestas.
Esta forma de verlo nos ayuda a entender la "distancia" angular entre las variables en un espacio multidimensional.
Galería de imágenes
-
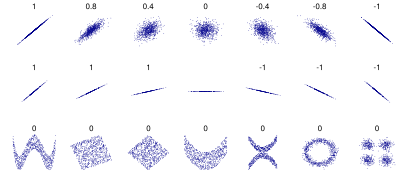
Varios conjuntos de puntos (x,y), con el coeficiente de correlación de Pearson de x e y para cada conjunto. La correlación refleja el ruido y la dirección de una relación lineal (fila superior), pero no la pendiente de esa relación (centro), ni muchos aspectos de las relaciones no lineales (parte inferior). N.B.: la figura del centro tiene una pendiente de 0 pero, en ese caso, el coeficiente de correlación no está definido porque la varianza de Y es cero.
Véase también
 En inglés: Correlation Facts for Kids
En inglés: Correlation Facts for Kids