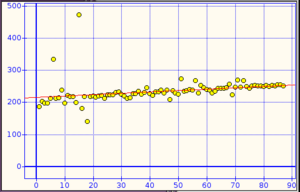
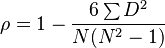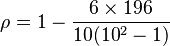Coeficiente de correlación de Spearman para niños
En estadística, el coeficiente de correlación de Spearman, representado con la letra griega ρ (ro), es una herramienta que nos ayuda a entender si dos grupos de datos están relacionados y cómo lo están. Imagina que tienes dos listas de números, por ejemplo, las calificaciones de un examen y las horas de estudio de varios estudiantes. El coeficiente de Spearman nos dice si hay una conexión entre esas dos cosas.
A diferencia de otras formas de medir la relación, el coeficiente de Spearman se enfoca en el orden o rango de los datos. Esto significa que no le importa tanto el valor exacto de cada número, sino la posición que ocupa ese número cuando los ordenamos de menor a mayor. Por ejemplo, si un estudiante sacó la mejor nota y también estudió la mayor cantidad de horas, eso es una buena señal de relación.
Para calcular este coeficiente, primero se ordenan los datos de cada lista y se les asigna un rango (1º, 2º, 3º, etc.). Luego, se comparan los rangos de cada par de datos para ver qué tan parecidos son.
El valor de ρ siempre estará entre -1 y +1:
- Si ρ es cercano a +1, significa que hay una relación positiva fuerte. Es decir, cuando una cosa aumenta, la otra también tiende a aumentar. Por ejemplo, más horas de estudio podrían relacionarse con mejores calificaciones.
- Si ρ es cercano a -1, significa que hay una relación negativa fuerte. Cuando una cosa aumenta, la otra tiende a disminuir. Por ejemplo, más horas de videojuegos podrían relacionarse con menos horas de sueño.
- Si ρ es cercano a 0, significa que no hay una relación clara entre los datos.
Contenido
¿Cómo se calcula el coeficiente de Spearman?
La fórmula para calcular ρ es:
Donde:
- D es la diferencia entre los rangos de cada par de datos.
- N es el número total de pares de datos que tienes.
Si hay datos que se repiten (tienen el mismo valor), se les asigna el promedio de los rangos que les corresponderían.
Ejemplo práctico del cálculo
Vamos a usar un ejemplo para entenderlo mejor. Imagina que queremos ver si hay una relación entre el Coeficiente Intelectual (CI) de algunas personas y las horas que ven televisión a la semana.
Aquí están los datos iniciales:
| CI | Horas de TV a la semana |
| 106 | 7 |
| 86 | 0 |
| 100 | 28 |
| 100 | 50 |
| 99 | 28 |
| 103 | 28 |
| 97 | 20 |
| 113 | 12 |
| 113 | 7 |
| 110 | 17 |
El primer paso es ordenar cada columna por separado y asignar un rango a cada valor. Si hay valores repetidos, se calcula el promedio de los rangos que les tocarían.
Por ejemplo, en la columna "CI":
- 86 es el más bajo, su rango es 1.
- 97 es el siguiente, su rango es 2.
- 99 es el siguiente, su rango es 3.
- 100 aparece dos veces. Si no se repitiera, ocuparían los rangos 4 y 5. Como se repiten, sumamos 4+5=9 y dividimos entre 2 (porque son dos valores), lo que da 4.5. Así, ambos valores de 100 tienen un rango de 4.5.
Hacemos lo mismo para la columna "Horas de TV a la semana":
- 0 es el más bajo, su rango es 1.
- 7 aparece dos veces. Sus rangos serían 2 y 3. El promedio es (2+3)/2 = 2.5.
- 12 es el siguiente, su rango es 4.
- 17 es el siguiente, su rango es 5.
- 20 es el siguiente, su rango es 6.
- 28 aparece tres veces. Sus rangos serían 7, 8 y 9. El promedio es (7+8+9)/3 = 8.
- 50 es el más alto, su rango es 10.
Ahora, creamos una tabla con los rangos y calculamos la diferencia (d) entre los rangos de cada par, y luego elevamos esa diferencia al cuadrado (d²).
| CI (i) | Horas de TV a la semana (t) | orden(i) | orden(t) | d (diferencia de rangos) | d² (diferencia al cuadrado) |
| 86 | 0 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | 4 | 16 |
| 99 | 28 | 3 | 8 | 5 | 25 |
| 100 | 50 | 4.5 | 10 | 5.5 | 30.25 |
| 100 | 28 | 4.5 | 8 | 3.5 | 12.25 |
| 103 | 28 | 6 | 8 | 2 | 4 |
| 106 | 7 | 7 | 2.5 | 4.5 | 20.25 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 113 | 7 | 9.5 | 2.5 | 7 | 49 |
| 113 | 12 | 9.5 | 4 | 5.5 | 30.25 |
Finalmente, sumamos todos los valores de la columna d²: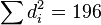 
. El número de pares de datos (N) es 10.
Ahora, sustituimos estos valores en la fórmula:
El resultado es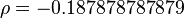 
.
Este valor de ρ (-0.1878...) es cercano a 0 y es negativo. Esto nos indica que, en este ejemplo, hay una relación muy débil y negativa entre el CI y las horas de televisión. Es decir, las personas con un CI más alto no necesariamente ven menos televisión, y viceversa, o la relación es casi inexistente.
¿Es significativa la relación?
Después de calcular el coeficiente de Spearman, es importante saber si la relación que encontramos es "real" o si podría ser solo una coincidencia. Esto se llama determinar la "significación estadística".
Existen métodos especiales, a menudo usando programas de computadora o tablas, para saber si el valor de ρ que calculamos es lo suficientemente grande (o pequeño, si es negativo) como para considerarlo una relación importante y no solo algo que ocurrió por casualidad. Si el valor es "significativo", significa que es muy probable que la relación exista en la realidad y no solo en nuestra pequeña muestra de datos.
Véase también
En inglés: Spearman's rank correlation coefficient Facts for Kids
Galería de imágenes
-
El coeficiente de correlación de Spearman es menos sensible que el de Pearson para los valores muy lejos de lo esperado. En este ejemplo: Pearson = 0.30706 Spearman = 0.76270
