Conjunto simplemente conexo para niños
Un espacio es simplemente conexo cuando está formado por una sola pieza y no tiene agujeros que lo atraviesen. Imagina una pelota de fútbol: puedes moverte por toda su superficie sin encontrar ningún agujero. Además, si dibujas un círculo en la superficie de la pelota, puedes encogerlo poco a poco hasta que se convierta en un punto, sin salirte de la superficie.
En el campo de las matemáticas llamado topología, que estudia las formas y los espacios, un espacio se considera simplemente conexo si cumple dos condiciones importantes:
- Está conectado por caminos: Esto significa que puedes ir de cualquier punto a otro punto dentro del espacio sin tener que salirte de él. Es como si todas sus partes estuvieran unidas.
- No tiene "agujeros" que lo atraviesen: Esto se refiere a que cualquier lazo (un camino que empieza y termina en el mismo lugar) que dibujes en el espacio, puede encogerse de forma continua hasta convertirse en un solo punto, sin salirse del espacio.
La idea de los espacios simplemente conexos es muy importante en un problema matemático famoso conocido como la Conjetura de Poincaré.
Contenido
¿Qué significa "simplemente conexo"?
Para entender mejor qué es un espacio simplemente conexo, piensa en objetos cotidianos. Un objeto es simplemente conexo si es una sola pieza y no tiene agujeros que lo atraviesen por completo. Por ejemplo, una pelota de baloncesto o una manzana son simplemente conexas.
Si dibujas un círculo en la superficie de una pelota, puedes "apretarlo" y encogerlo hasta que sea un punto, sin salirte de la superficie de la pelota. Esto es lo que significa que un lazo se puede contraer a un punto.
Ejemplos de espacios simplemente conexos
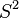es simplemente conexa ya que es conexa por caminos y todo lazo puede contraerse continuamente sobre la superficie a un punto.- El espacio donde vivimos: El espacio tridimensional que nos rodea, o un plano, o una línea recta, son ejemplos de espacios simplemente conexos. No tienen agujeros y todas sus partes están conectadas.
- La superficie de una esfera: La superficie de una pelota (como la Tierra o una pelota de fútbol) es simplemente conexa. Puedes moverte por toda ella y cualquier lazo que dibujes se puede encoger a un punto.
- Cualquier forma sin agujeros: Un cubo, una pirámide o un cilindro sólido (sin agujero en el centro) son simplemente conexos.
Ejemplos de espacios NO simplemente conexos
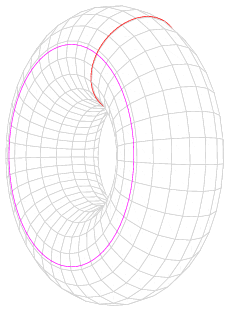
- Un anillo o una rosquilla: Estos objetos tienen un agujero en el centro. Si dibujas un lazo alrededor del agujero, no puedes encogerlo a un punto sin salirte del objeto. Por eso, no son simplemente conexos.
- El espacio sin un punto: Si tomas un plano y le quitas un solo punto, el espacio resultante ya no es simplemente conexo. Aunque sigue estando conectado, el punto que falta crea un "agujero" que impide que ciertos lazos se encojan.
- La superficie de un toro: Un toro es la forma de una rosquilla o un flotador. Su superficie tiene un agujero en el centro. Si dibujas un lazo que rodea ese agujero, no puedes encogerlo a un punto sin salirte de la superficie. Por lo tanto, no es simplemente conexo.
Ver también
- Homotopía
- Espacio conexo por caminos
- Conjetura de Poincaré
Enlaces externos
- Weisstein, Eric W. «SimplyConnected». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
de:Zusammenhängender Raum#Einfach zusammenhängend
Véase también
En inglés: Simply connected space Facts for Kids
