Circuito RLC para niños
Un circuito RLC es un tipo de circuito eléctrico que combina tres componentes básicos: una resistencia eléctrica (R), una bobina (L) y un capacitor (C). Estos circuitos son muy importantes en la electrónica porque pueden hacer cosas interesantes con la electricidad, como seleccionar ciertas frecuencias de señales.
Existen dos formas principales de conectar estos componentes: en serie o en paralelo. El comportamiento de un circuito RLC es más complejo que el de otros circuitos más sencillos, como los que solo tienen resistencia y capacitor (RC) o resistencia y bobina (RL).
Una característica especial de los circuitos RLC es que pueden mostrar un fenómeno llamado resonancia. Esto ocurre cuando el circuito responde de forma muy fuerte a una frecuencia específica de la señal eléctrica que se le aplica. Es como empujar un columpio: si lo empujas al ritmo adecuado (su frecuencia de resonancia), el columpio subirá muy alto.
Contenido
¿Qué son los componentes de un circuito RLC?
Para entender un circuito RLC, primero debemos saber qué hace cada una de sus partes:
La Resistencia (R)
La resistencia es un componente que se opone al paso de la corriente eléctrica. Imagina que es como un estrechamiento en una tubería de agua: hace que el agua (la corriente) fluya con más dificultad. Se mide en ohmios (Ω).
La Bobina (L)
La bobina (también llamada inductor) es un cable enrollado que almacena energía en un campo magnético cuando la corriente pasa por ella. Es como una pequeña batería que reacciona a los cambios de corriente. Se mide en henrios (H).
El Capacitor (C)
El capacitor (o condensador) es un componente que almacena energía en un campo eléctrico. Piensa en él como un pequeño depósito de agua que puede llenarse y vaciarse de electricidad. Se mide en faradios (F).
Tipos de circuitos RLC
Los circuitos RLC se pueden conectar de dos maneras principales:
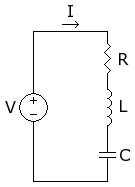
Circuito RLC en serie
En un circuito RLC en serie, la resistencia, la bobina y el capacitor están conectados uno tras otro, formando un único camino para la corriente eléctrica. Esto significa que la misma corriente fluye a través de cada uno de los componentes.
¿Cómo funciona la resonancia en serie?
Cuando una señal eléctrica con una frecuencia específica (llamada frecuencia de resonancia) se aplica a un circuito RLC en serie, la corriente en el circuito se vuelve muy grande. Esto sucede porque los efectos de la bobina y el capacitor se cancelan entre sí a esa frecuencia, dejando solo la resistencia para limitar la corriente. La frecuencia de resonancia (f0) se puede calcular con la fórmula:
- f0 = 1 / (2π√LC)
Donde L es la inductancia de la bobina y C es la capacidad del capacitor.
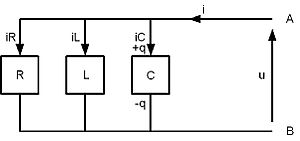
Circuito RLC en paralelo
En un circuito RLC en paralelo, la resistencia, la bobina y el capacitor están conectados en diferentes ramas, de modo que la corriente se divide entre ellos. En este caso, el voltaje es el mismo en cada componente.
¿Cómo funciona la resonancia en paralelo?
En un circuito RLC en paralelo, la resonancia también ocurre a la misma frecuencia que en el circuito en serie (f0 = 1 / (2π√LC)). Sin embargo, en este caso, la corriente total que entra al circuito se vuelve muy pequeña a la frecuencia de resonancia, porque la corriente se "circula" entre la bobina y el capacitor, sin pasar por la fuente de energía.
Usos de los circuitos RLC
Los circuitos RLC son muy útiles en muchas aplicaciones electrónicas:
- Filtros de frecuencia: Pueden usarse para dejar pasar solo ciertas frecuencias de señales y bloquear otras. Por ejemplo, en una radio, un circuito RLC ayuda a sintonizar una emisora específica, dejando pasar solo la frecuencia de esa emisora y eliminando el ruido de otras.
- Sintonizadores: Se usan en radios y televisores para seleccionar la frecuencia de la señal que queremos escuchar o ver.
- Osciladores: Pueden generar señales eléctricas que vibran a una frecuencia específica, lo cual es útil en muchos dispositivos electrónicos.
- Transformadores de impedancia: Ayudan a adaptar la "resistencia" de un circuito a otro para que la energía se transfiera de la manera más eficiente posible.
Cuando un circuito tiene varias bobinas y capacitores, se le llama "red LC". Un circuito RLC simple se considera de "segundo orden" porque su comportamiento se describe con ecuaciones matemáticas que tienen un término de segundo grado.
Galería de imágenes
Véase también
 En inglés: RLC circuit Facts for Kids
En inglés: RLC circuit Facts for Kids
- Circuito RC
- Circuito RL
- Circuito LC